Характеристики предприятий Всеволожского района Ленинградской области в 1995 г.
| Предприятия | Значения признаков | В % к средней | Многомер-ная средняя, % | ||||||
| х1 | х2 | х3 | х4 | х1 | х2 | х3 | х4 | ||
| «Ручьи» | 20,6 | ||||||||
| «Бугры» | 12,1 | ||||||||
| «Пригородное» | 20,6 | ||||||||
| «Авлога» | 15,1 | ||||||||
| «Всеволожское» | 14,8 | ||||||||
| «Выборгское» | 24,0 | ||||||||
| «Приневское» | 33,2 | ||||||||
| «Шеглово» | 15,0 | ||||||||
| Средние величины | 19,4 | ||||||||
| Средние квадратические отклонения | 6,4 | - | - | - | - | - |
Судя по полученным оценкам, предприятия делятся на группы с многомерными средними ниже 100% (четыре предприятия), несколько выше 100% (два предприятия) и резко превышающие 100% (два предприятия).
При большом 'объеме совокупности для выделения группнаоснове многомерной средней необходимо установить интервалы значений многомерной средней;
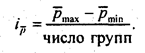
Затем следует провести группировку единиц: определить их количество в каждой группе и постараться указать, в чем состоят качественные различия между группами.
Более обоснованным методом многомерной классификации является кластерный анализ. Само название метода происходит от того же корня, что и слово «класс», «классификация». Английское слово the cluster имеет значения: группа, пучок, куст, т. е. объединений каких-то однородных явлений. В данном контексте оно близко к математическому понятию «множества», причем, как и множество, кластер может содержать только одно явление, но не может в отличие от множества быть пустым.
Каждая единица совокупности в кластерном анализе рассматривается как точка в заданном признаковом пространстве. Значение каждого из признаков у данной единицы служит ее координатой в этом «пространстве» по аналогии с координатами точки в нашем реальном трехмерном пространстве. Таким образом, признаковое пространство - это область варьирования всех признаков совокупности изучаемых явлений. Если мы уподобим это пространство обычному пространству, имеющему евклидову метрику, то тем самым мы получим возможность измерять «расстояния» между точками признакового пространства. Эти расстояния называют евклидовыми. Их вычисляют по тем же правилам, как и в обычной евклидовой геометрии. На плоскости, т.е. в двухмерном пространстве, расстояние между точками А и В равно корню квадратному из суммы квадратов разностей координат этих точек по оси абсцисс и по оси ординат - на основании теоремы Пифагора (рис. 6.1).

Рис. 6.1. Евклидово расстояние
В многомерном признаковом пространстве расстояние между точками р и q с k координатами, т. е. индивидуальными значениями k признаков, определяется так:
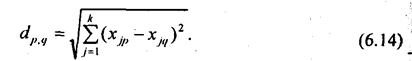
Совершенно очевидно, что нельзя суммировать квадраты отклонений одной точки от другой в абсолютных значениях разнокачествен-ных признаков. Необходимо сначала выразить различия между единицами совокупности по каждому признаку в каком-то относитель,но безразмерном показателе. В качестве такого показателя часто применяют «нормированную разность», т. е. величину:


По данным табл. 6.8 среднее квадратическое отклонение признака х, равно 109. Разделив все попарные разности значений этого признака на 109, получим матрицу нормированных разностей D1 (табл. 6.9). Очевидно эта матрица размером п×п симметрична.
Таблица 6.9
Дата добавления: 2015-01-21; просмотров: 998;
