Виведення розрахункової формули
Знайдемо залежність опору чистого напівпровідника від температури.
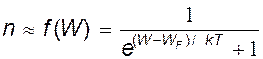 |
Концентрація електронів у зоні провідності пропорційна ймовірності перебування їх у цій зоні, тобто функції розподілу Фермі–Дірака:
Як показують розрахунки, рівень Фермі в чистому напівпровіднику
при T=0 розташований посередині забороненої зони (рис.5). Якщо в чистому напівпровіднику відраховувати енергію від стелі валентної зони, то W-WF=DW/2, де DW – ширина забороненої зони. Оскільки електропровідність g пропорційна концентрації електронів n, то
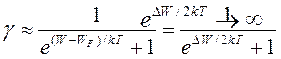 |
В області низьких температур (Т®0) значення експоненти
тому g=0. тобто при низьких температурах напівпровідник поводиться як діелектрик.
В області кімнатних температур значення експоненти eDW/2kТ значно більше одиниці. Тому нехтуючи одиницею в знаменнику, одержимо:
тобто з підвищенням температури електропровідність напівпровідників
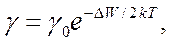 |
зростає. Механізм такого росту зв'язаний з тим, що з підвищенням температури збільшується концентрація вільних електронів у зоні провідності. Оскільки опір R обернено пропорційний електропровідності, то
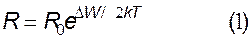 |
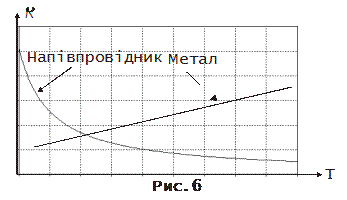
тобто з підвищенням температури опір напівпровідника падає (рис.6).
У той же час опір металів з підвищенням температури зростає:
R=  R0(1+a t) (2)
R0(1+a t) (2)
де a - температурний коефіцієнт опору, а t – температура в шкалі Цельсія. Це зв'язано з тим, що з підвищенням температури зростає число зіткнень електронів з іонами кристалічної ґратки, амплітуда коливань яких збільшується з ростом Т. Помітимо, що такий механізм є універсальним, однак, для напівпровідників він не грає істотної ролі, тому що тут домінуючим є процес зростання концентрації вільних носіїв струму з підвищенням температури.
Метою роботи є дослідження температурної залежності опору напівпровідника і металу.
Напівпровідникові опори (термістори) – прилади, у яких використовується істотна зміна опору зі зміною температури, у зв'язку з чим вони знаходять широке застосування з метою регулювання процесів, де необхідний температурний контроль.
Визначивши залежність опору напівпровідника від температури, можна розрахувати ширину забороненої зони. Для цього прологарифмуємо вираз (1), запишемо його для двох різних температур і візьмемо різницю. В результаті одержимо:
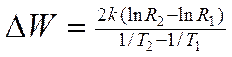
| (3) |
де 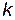 =1.38 ×10-23 Дж/K – стала Больцмана.
=1.38 ×10-23 Дж/K – стала Больцмана.
Важливою характеристикою провідника є температурний коефіцієнт опору, що визначає відносну зміну опору при підвищенні температури на 1К:
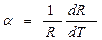
| (4) |
 Взявши похідну від виразу (1), одержимо для термоопору:
Взявши похідну від виразу (1), одержимо для термоопору:
aтерм = -DW/(2kТ2) (5)
Знак “мінус” у виразі (5) означає, що з підвищенням температури опір термістора зменшується.
З врахуванням того, що для металу залежність R від T є лінійною, вираз (4) можна перетворити до вигляду:
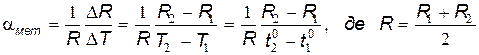
| (6) |
3. Експериментальна частина (варіант №1)
Досліджувані напівпровідниковий і металевий опори поміщені в термостат з нагрівачем, мішалкою і термометром. Спочатку в термостаті встановлюється кімнатна температура, при якій вимірюють опір термістора і металу. Потім включають на якийсь час нагрівач і, піднявши температуру в ньому на 5-70С, знову вимірюють опір. Такі виміри опорів через кожні 5-70С продовжують до 50-600С, зробивши не менше 10 вимірів. У процесі вимірів повинна безупинно працювати мішалка термостата. Опори термістора і металу вимірюють, використовуючи нульовий метод моста постійного струму.
Результати вимірювань заносять в таблицю.
| № | t,0C | T, K | 1/T ´10-3 | Термоопір | Метал | |||||
| Rет, Ом | Відношення плеч | Rтерм Ком | lnR | Rет Ом | Відношения плеч | Rмет Ом | ||||
| …… | …… …… | …… …… | …… | …… …… | ………… | ………… | …… …… | …… …… | …… …… | …… …… |
Дата добавления: 2015-01-15; просмотров: 1312;
