Приближение при помощи показательной функции
Если расположение опытных точек похоже на расположение точек графика показательной функции, то ищем эмпирическую формулу в виде
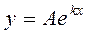
| (4.6) |
Если нанесем опытные точки на полулогарифмическую бумагу и они расположатся приблизительно на прямой линии, то мы окончательно убедимся в том, что зависимость y(x) выражается именно показательной функцией.
Для нахождения A и k можно применить метод выбранных точек. Для этого прологарифмируем равенство (4.6).
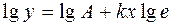
Полагая здесь 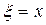 ,
, 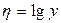 и обозначая
и обозначая 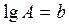 ,
, 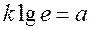 , приходим к уравнению
, приходим к уравнению
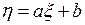 (4.7)
(4.7)
Зависимость (4.7) – это линейная функция. Для отыскания a и b можно применить один из рассмотренных выше способов. Но лучше всего воспользоваться методом средней (труднее ошибиться). В уравнении (4.7) возвратимся к старым переменным х и у и запишем его в виде
ах + b – lg y = 0 (4.8)
Делим все опытные точки на две группы и для каждой группы сумму невязок уравнения (4.8) приравниваем 0. Получаем систему двух уравнений с неизвестными а и b. Найдя а и b, находим А и k.
Пример. На основании опытных данных результаты разрядки конденсатора U(t) даются таблицей 3.
Таблица 3:
| t | |||||||||||
| U |
Если бы мы построили опытные точки на полулогарифмической бумаге, то убедились бы, что они располагаются приблизительно на прямой. Значит зависимость U(t) можно выразить формулой (4.6). Воспользуемся методом средней. Для этого равенство (4.8) запишем через переменные U и t
at + b – lg U = 0.
Здесь, как и прежде b = lg A, a = k lg e.
Разбиваем все опытные точки на две группы. В первую группу включаем первые шестьточек, во вторую – остальные пять точек. Найдём сумму невязок в первой группе и во второй группе и приравняем их к 0
b – lg 100 + a + b – lg 75 + 2a + b – lg 55 + 3a + b – lg 40 + 4a + b – lg 30 + +5a + b – lg 20 = 15a + 6b = 10.
6a + b – lg 15 + 7a +b – lg 10 + 8a+ b – lg 10 + 9a +b – lg 5 + 10a + b –lg 5 = =40a + 5b = 4,57.
После приведения всех подобных, получаем систему двух уравнений
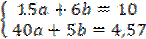 |
| 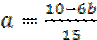
80 – 48b + 15b = 13,71;
33b = 66,3.
b = 2,01, a = 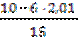 = - 0,133,
= - 0,133,
k = 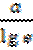 =
= 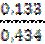 = – 0,31,
= – 0,31,
2,01 = lg a; a = 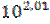 = 102,3.
= 102,3.
Таким образом, эмпирическая формула будет иметь вид
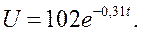
Дата добавления: 2015-02-03; просмотров: 1082;
