Эмпирические формулы, содержащие три параметра.
В этом случае эмпирические формулы в общем виде записываются так
y = f(x; a,b,c),
где a, b и с – некоторые постоянные.
Первой формулой с тремя параметрами является квадратическая зависимость
y= ax2 + bx + c. (4.21)
Критерий проверки экспериментальных данных на зависимость (4.21) существует. Но он строится с таки громоздкими расчётами и составлением сложной таблицы, что легче по экспериментальным данным построить кривую, как мы это уже делали, и убедиться, похожа ли она на зависимость (4.21).
Рассмотрим степенную зависимость вида
y = axb + c (4.22)
Отсюда y – c = axb. Логарифмируя это выражение получим
lg (y – c) = lg a +b lg x.
Полагая lg (y - c) = Y и lg x = X, получим линейную зависимость
Y = bX + lg a.
Определение параметров формулы (4.22) начнём с нахождения с. Для этого составим среднее геометрическое 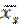 =
= 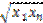 , и, пользуясь графиком, построенным по исходным данным, или методом линейной интерполяции для
, и, пользуясь графиком, построенным по исходным данным, или методом линейной интерполяции для 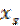 , найдём соответствующее значение
, найдём соответствующее значение 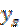 . Предполагая, что точки M1(x1, y1), MS(xS, yS), Mn(xn, yn) расположены на кривой (4.22), будем иметь три неравенства.
. Предполагая, что точки M1(x1, y1), MS(xS, yS), Mn(xn, yn) расположены на кривой (4.22), будем иметь три неравенства.
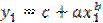 ,
, 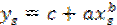 ,
, 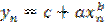 .
.
Возводя 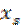 =
= 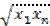 в степень b и умножая на а, получим
в степень b и умножая на а, получим
a 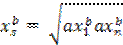 или ys – c =
или ys – c = 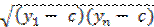 .
.
Решим последнее уравнение относительно с.
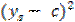 =
= 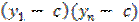 ;
; 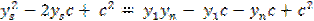 ;
;
c ( 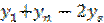 ) =
) = 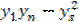 ; c =
; c = 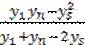 .
.
После этого строим точки Ni(Xi, Yi) , где Xi = lg xi, Yi = lg(yi – c) (i = 1,2,…, n). Если эти точки располагаются близко к прямой линии, то зависимость (4.22) выбрана правильно. Причём, постоянные а и b находятся обычным способом.
Пример. Для переменных х и у дана таблица 12
Таблица 12
| х | ||||||
| у | 0,10 | 0,28 | 0,80 | 1,38 | 2,56 | 4,10 |
Найти эмпирическую формулу, связывающую эти переменные коэффициентами a,b и с.
Решение. Построим эмпирическую формулу вида:
y = axb + c.
Находим
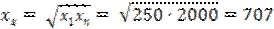 .
.
На графике, если его построить, этому значению соответствует 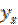 = 0,507. Отсюда
= 0,507. Отсюда
c = 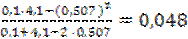 .
.
Остальные параметры а и b найдём методом средних.
Составляем начальное уравнение с учетом, найденного значения с.
lg (yi – 0,048) = lg a + b lg xi, (i = 1,2,…,6)
Тогда будем иметь систему уравнений
-1,2840 = lg a+ 2,3979b; 0,1245 = lg a + 3,0792b;
-0,6345 = lg a + 2,6990b; 0,4000 = lg a + 3,2041b;
-0,1238 = lg a + 2,9542b; 0,6077 = lg a + 3,3010b;
Группируя эти уравнения по три, получим
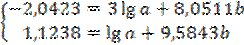 .
.
Вычитаем из первого уравнения второе: -3,1745 = 1,5332b; b = 2,071.
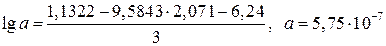 .
.
Таким образом, искомая эмпирическая формула будет иметь вид.
y = 5,75 · 10-7x2,071 + 0,048.
Рассмотрим показательную зависимость
y = aebx + c (4.23)
Перенося слагаемое с влево и логарифмируя, получим
lg (y - c) = lg a + bxM,
где M = lg e = 0,434.
Таким образом,
Y = lg a + bMx, (4.24)
где y = lg(y – c).
Определим параметр с. Для этого, как и в предыдущем случае, выберем крайние точки M1(x1, y1) и Mn(xn, yn) и составим среднее арифметическое
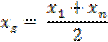
Для 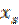 найдём соответствующее
найдём соответствующее 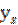 (или из чертежа, или линейной интерполяцией). Представляя эти значения в эмпирическую формулу (4.23), будем иметь
(или из чертежа, или линейной интерполяцией). Представляя эти значения в эмпирическую формулу (4.23), будем иметь
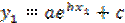 ;
; 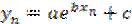 ;
; 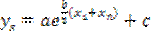 .
.
Отсюда 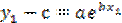 ;
; 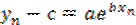 ;
; 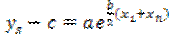 . Следовательно
. Следовательно
( 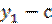 )(
)( 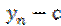 ) =
) = 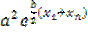 ; (
; ( 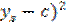 =
= 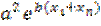 ;
;
( 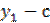 )(
)( 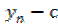 ) =(
) =( 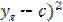 .
.
Получим точно такое же уравнение, как и в предыдущем случае.
Поэтому с запишем в таком же виде
с = 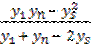 .
.
Если обнаружена линейная зависимость (4.24), то остальные параметры а и b находятся обычными приёмами.
Пример. Дана таблица 13
Таблица 13
| х | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | |
| у | 1,30 | 1,44 | 1,59 | 1,78 | 1,97 | 2,19 | 2,46 | 2,74 | 3,06 | 3,42 | 3,84 |
Найти эмпирическую формулу. Будем её искать в виде
y = aebx + c.
сначала найдём 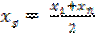 =
= 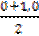 = 0,5. Этому значению
= 0,5. Этому значению 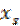 в данной таблице соответствует значение
в данной таблице соответствует значение 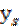 = 2,19. Отсюда
= 2,19. Отсюда
с = 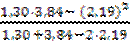 = 0,258.
= 0,258.
Параметры а и b определяем по методу средних. Для этого запишем
lg (yi – 0.258) = lg a + bMxi, (i = 1,2,…,10).
Составим две системы уравнений
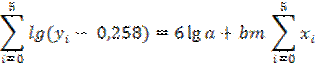
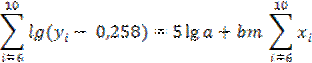
Подставив значения xi и yi и приведя подобные члены, получим систему двух уравнений
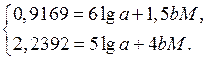
Решая эту систему найдём: а = 1,044; b = 1,234. Следовательно, эмпирическая формула имеет вид
у = 1,044е1,234х+0,258.
Дата добавления: 2015-02-03; просмотров: 1093;
