Приближение при помощи степенной функции
При изучении многих явлений эмпирическую формулу удобно представить в виде степенной функции.
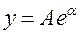 (4.9)
(4.9)
Признаком того, что именно такая функция выражает зависимость между данными величинами, является расположение опытных точек по прямой линии в логарифмической системе координат.
Пример. Даны табличные значения x и y
| х | ||||||||
| у | 1,06 | 1,33 | 1,52 | 1,68 | 1,81 | 1,91 | 2,01 | 2,11 |
Не трудно предположить, что они соответствуют формуле (4.9). Действительно, если данные точки нанести на логарифмическую систему координат, то они с достаточной точностью располагаются на прямой линии. Тем самым подтверждается наше предположение, что зависимость у(х) соответствует выражению (4.9).
Для определения параметров а и 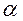 выберем крайней точки А(10;1,06) и В(80;2,11).
выберем крайней точки А(10;1,06) и В(80;2,11).
Логарифмируя выражение (4.9), получим
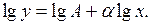
Представляя координаты точек А и В, находим
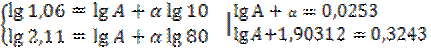
Отсюда –α + 0,0253 = – 1,90312 + 0,3243; 0,9031 α = 0,2990
α = 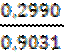 = 0,3311.
= 0,3311.
lg A = 0,0253 – 0,3311 = – 0,3058, A = 10-0,3058 = 0,4945.
Таким образом,
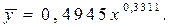
Таблица проверки:
| х | ||||||||
| у | 1,06 | 1,33 | 1,52 | 1,68 | 1,8 | 1,92 | 2,01 | 2,11 |
Сравнивая исходную таблицу с таблицей проверки, построенной по полученной эмпирической формуле, видим, что они практически совпадают.
Дата добавления: 2015-02-03; просмотров: 1203;
