Основные формулы. где F - сила взаимодействия точечных зарядов и ; - расстояние между зарядами; - диэлектрическая проницаемость; -электрическая постоянная.
Закон Кулона:
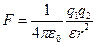
где F - сила взаимодействия точечных зарядов 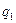 и
и 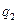 ;
; 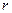 - расстояние между зарядами;
- расстояние между зарядами; 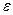 - диэлектрическая проницаемость;
- диэлектрическая проницаемость; 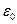 -электрическая постоянная.
-электрическая постоянная.
Напряженность электрического поля и потенциал:
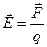
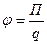
где П - потенциальная энергия точечного положительного заряда q, находящегося в данной точке поля (при условии, что потенциальная энергия заряда, удаленного в бесконечность, равна нулю).
Сила, действующая на точечный заряд, находящийся в электрическом поле, и потенциальная энергия этого заряда:
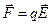
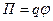
Напряженность и потенциал поля, создаваемого системой точечных зарядов (принцип суперпозиции электрических полей):
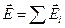
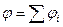
где 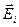 ,
, 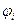 - напряженность и потенциал в данной точке поля, создаваемого i-м зарядом.
- напряженность и потенциал в данной точке поля, создаваемого i-м зарядом.
Напряженность и потенциал поля, создаваемого точечным зарядом:
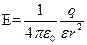
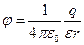
где 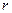 - расстояние от заряда q до точки, в которой определяются напряженность и потенциал.
- расстояние от заряда q до точки, в которой определяются напряженность и потенциал.
Напряженность и потенциал поля, создаваемого проводящей заряженной сферой радиусом R на расстоянии 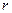 от центра сферы:
от центра сферы:
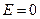
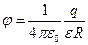 , (при r < R)
, (при r < R)
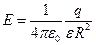
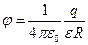 , (при r=R)
, (при r=R)
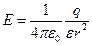
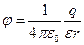 (при r>R)
(при r>R)
где q – заряд сферы.
Линейная плотность заряда:
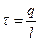
Поверхностная плотность заряда:
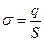
Напряженность и потенциал поля, создаваемого распределенными зарядами. Если заряд равномерно распределен вдоль линии с линейной плотностью 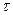 , то на линии выделяется малый участок длиной
, то на линии выделяется малый участок длиной 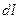 с зарядом
с зарядом 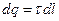 . Такой заряд можно рассматривать как точечный и применять формулы:
. Такой заряд можно рассматривать как точечный и применять формулы:
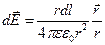
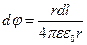
где r - радиус-вектор, направленный от выделенного элемента dl к точке, в которой вычисляется напряженность.
Используя принцип суперпозиции электрических полей, находим интегрированием напряженность 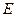 и потенциал φ поля, создаваемого распределенным зарядом:
и потенциал φ поля, создаваемого распределенным зарядом:
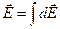
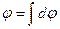
Интегрирование ведется вдоль всей длины l заряженной линии.
Напряженность поля, создаваемого бесконечной прямой равномерно заряженной нитью или бесконечно длинным цилиндром:
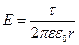
где r - расстояние от нити или оси цилиндра до точки, напряженность поля в которой вычисляется.
Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью:
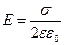
Связь потенциала с напряженностью:
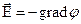 , или
, или 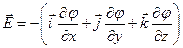 (в общем случае),
(в общем случае),
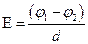 , (в случае однородного поля);
, (в случае однородного поля);
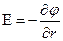 (в случае поля, обладающего центральной или осевой симметрией).
(в случае поля, обладающего центральной или осевой симметрией).
Электрический момент диполя:
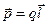 ,
,
где q - заряд; 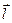 - плечо диполя (векторная величина, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами).
- плечо диполя (векторная величина, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами).
Работа сил поля по перемещению заряда q из точки поля с потенциалом 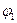 в точку с потенциалом
в точку с потенциалом 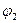 :
:
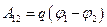
Электроемкость:
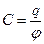 или
или 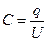 ,
,
где 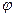 - потенциал проводника (при условии, что в бесконечности потенциал проводника принимается равным нулю); U
- потенциал проводника (при условии, что в бесконечности потенциал проводника принимается равным нулю); U  - разность потенциалов пластин конденсатора.
- разность потенциалов пластин конденсатора.
Электроемкость уединенной проводящей сферы радиусом R:
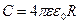
Электроемкость плоского конденсатора:
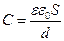
где S - площадь пластины конденсатора; d - расстояние между пластинами.
Электроемкость батареи конденсаторов:
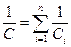 (при последовательном соединении)
(при последовательном соединении)
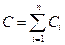 (при параллельном соединении),
(при параллельном соединении),
где n -число конденсаторов в батарее.
Энергия заряженного конденсатора:
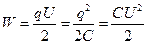
Сила тока: 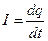 ,
,
где 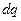 - заряд, прошедший через поперечное сечение проводника за время
- заряд, прошедший через поперечное сечение проводника за время 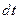 .
.
Плотность тока:
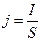 ,
,
где S - площадь поперечного сечения проводника.
Связь плотности тока со средней скоростью 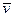 направленного движения заряженных частиц:
направленного движения заряженных частиц:
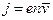 ,
,
где е - заряд частицы; n - концентрация заряженных частиц.
Закон Ома:
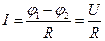 (для участка цепи, не содержащего э.д.с.)
(для участка цепи, не содержащего э.д.с.)
где 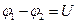 - разность потенциалов (напряжение) на концах участка цепи; R - сопротивление участка;
- разность потенциалов (напряжение) на концах участка цепи; R - сопротивление участка;
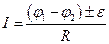 (для участка цепи, содержащего э.д.с),
(для участка цепи, содержащего э.д.с),
где 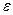 - э.д.с. источника тока; R - полное сопротивление участка цепи.
- э.д.с. источника тока; R - полное сопротивление участка цепи.
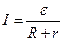 (для замкнутой цепи),
(для замкнутой цепи),
где R - внешнее сопротивление цепи; r - внутреннее сопротивление цепи.
Законы Кирхгофа:
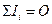 , (первый закон);
, (первый закон);
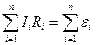 , (второй закон),
, (второй закон),
где 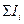 - алгебраическая сумма токов, сходящихся в узле;
- алгебраическая сумма токов, сходящихся в узле; 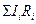 - алгебраическая сумма падений напряжения в контуре;
- алгебраическая сумма падений напряжения в контуре; 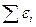 - алгебраическая сумма э.д.с., действующих в контуре.
- алгебраическая сумма э.д.с., действующих в контуре.
Сопротивление R и проводимость G проводника:
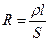 ;
; 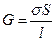
где 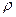 - удельное сопротивление;
- удельное сопротивление; 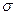 - удельная проводимость;
- удельная проводимость;  l - длина проводника;
l - длина проводника; 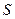 - площадь поперечного сечения проводника.
- площадь поперечного сечения проводника.
Сопротивление системы проводников:
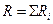 (при последовательном соединении);
(при последовательном соединении);
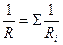 (при параллельном соединении),
(при параллельном соединении),
где 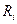 - сопротивление i-гo проводника.
- сопротивление i-гo проводника.
Работа силы тока:
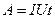 ;
; 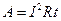 ;
; 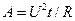 .
.
Мощность тoкa:
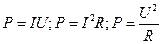
Закон Джоуля-Ленца:
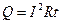
Закон Ома в дифференциальной форме:
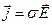
где 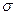 - удельная проводимость,
- удельная проводимость, 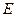 - напряженность электрического поля,
- напряженность электрического поля, 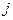 - плотность тока.
- плотность тока.
Связь удельной проводимости с подвижностью 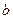 заряженных частиц (ионов):
заряженных частиц (ионов):
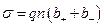 ,
,
где q -заряд иона; n -концентрация ионов; 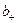 и
и 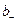 - подвижности положительных и отрицательных ионов.
- подвижности положительных и отрицательных ионов.
Дата добавления: 2015-01-13; просмотров: 1114;
