И обратная зависимость

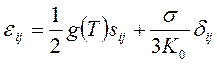, (2.78)

которые являются простым обобщением уравнений (2.73) – (2.75).

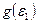В уравнениях (2.76) – (2.78) функция g(Г) в силу соотношения и формулы (2.67) определяется по виду функции , например, подобно формуле (2.68):

.

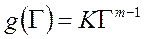Функция 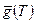служит коэффициентом в обратном соотношении 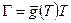: например, для степенного закона (2.68)

,

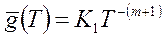где .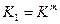

В случае несжимаемого тела (v = 0,5) уравнения состояния принимают вид

.

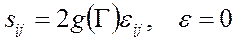В состояния пластического течения (см. рис.12 участок АВ), например, при обобщенном критерии Губера – Мизеса, характеризующим переход к пластическим деформациям,

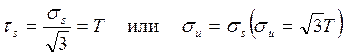, (2.79)

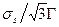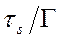в уравнениях (2.76) и (2.77) функцию g(Г) необходимо принять или , где 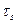- интенсивность напряжений [см. формулу (1.41)]. В этом случае нельзя однозначно определить компоненты деформации 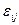, подобно формуле (2.78), что вполне естественно, если обратить внимание на участок АВ (см. рис. 12), где нет взаимно однозначного соответствия между 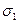и .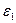

3. Критерий прочности при кратковременном монотонном нагружении.

Критерий прочности при кратковременном монотонном нагружении – это есть условие перехода какого-либо элемента нагруженного твердого тела в состояние хрупкого разрушения или пластического течения, когда в известной мере исчерпывается несущая способность.
При одноосном напряженном состоянии критерий прочности оценивается предельным, или опасным, значением напряжения; например, на рис. 12 это 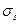или 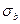. При переходе к сложному напряженному состоянию исходят из простейшего естественного предположения: уравнение предельного состояния не должно зависеть от выбора системы координат и должно содержать лишь инварианты, характеризующие напряженное состояние. Согласно выводам лекции 1.2, этими инвариантами будут T – интенсивность касательных напряжений; 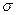- среднее нормальное напряжение; 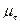- параметр Лоде – Надаи. Поэтому в общем случае критерий прочности определяется некоторой предельной поверхностью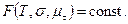

Предложено много различных критериев прочности при сложно-напряженном состоянии изотропных тел. В инженерных расчетах чаще других применяют критерий Шлейхера – Надаи

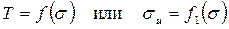, (2.80)

где вид функции в правой части устанавливается экспериментально по данным опытов для конкретных материалов.

В частности, при 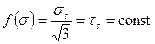из (2.70) следует критерий Губера – Мизеса (2.79) или эквивалентный ему по форме энергетический критерий. Оба этих критерия основаны на гипотезе, по которой процесс разрушения зависит главным образом от изменения формы элемента тела.

При достижении потенциальной энергией формоизменения элемента тела предельного состояния наступает его разрушение или переход к пластической деформации.

Если , то из условия (2.80) следует обобщенный критерии Мора 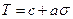. Используя формулы разд.2, критерий (2.80) можно сформулировать в терминах максимального касательного 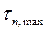и нормального напряжений:

.

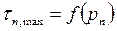Например, относительно главных координатных осей при условии 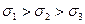, обобщая соотношение (2.71), можно принять

.

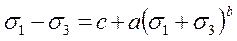Иногда в качестве критерия разрушения используются ограничения деформаций.

Изучая механическое поведение горных пород, надо иметь в виду присущие им важные особенности: с одной стороны, деформационную и прочностную анизотропию, обусловленную слоистостью, сланцеватостью или направленной трещиноватостью их строения, а с другой – наличием пор или трещин, заполненных пластовой жидкостью, газом или их смесью.

4. Трансверсально-изотропные тела(свойства анизотропии горных пород в плоскости, параллельной напластованию).

При изучении анизотропии горных пород чаще всего ограничиваются изучением свойств горных пород в плоскости, параллельной напластованию, и плоскости, перпендикулярной к напластованию, считаю любое из направлений в этих плоскостях эквивалентным в отношении механических свойств.

Такие тела принято называть трансверсально-изотропными. Ниже приведены упругие постоянные некоторых горных пород, заимствованные из разных литературных источников: Е, Е’ – модули Юнга по направлениям, параллельным напластованию и перпендикулярным к ним; v, v’ – коэффициенты Пуассона, характеризующие поперечное сжатие в плоскости напластования при сжатии в той же плоскости и в направлении, перпендикулярном к ней.

Если координатная плоскость 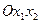выбрана параллельно плоскости напластования, а ось 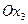- перпендикулярно к ней, то обобщенный закон Гука записывается в виде:

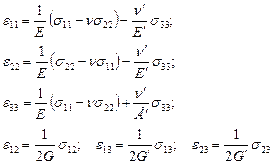(2.81)

где 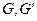- модули сдвига в плоскости 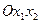и в перпендикулярных к ней плоскостях.

Упругие постоянные горных пород	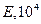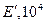МПа	МПа
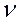
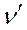
Алевролит	6,21	5,68	0,29	0,26
Глинистые сланцы	3,16	1,54	0,22	0,22
Песчаник	1,57	0,96	0,21	0,28
Песчанистый сланец	1,07	0,52	0,41	0,20