Обратная задача

Пусть о решении прямой задачи (1)-(4) известна дополнительная информация

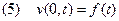
Требуется определить один из коэффициентов уравнения (1) (или какую-либо их комбинацию) из соотношений (1)-(5).

Численное решение обратной задачи (1)-(5) будем искать при 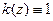, минимизируя целевой функционал

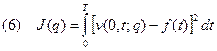
Зададим начальное приближение .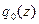

Приближение 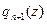будем вычислять методом простой итерации

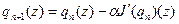
Здесь 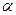- достаточно малое число, 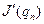- градиент функционала .

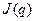Обратная задача 1: найти коэффициент 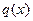из соотношений:

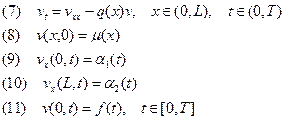
Найдем приращение функционала (6):

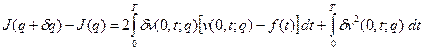
Здесь 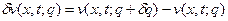. 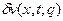является решением следующей задачи

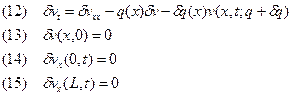
Рассмотрим сопряженную задачу:

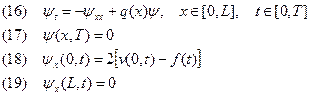
Умножим обе части равенства (12) на функцию 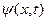и проинтегрируем по области :

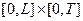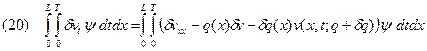
Проинтегрируем по частям выражение

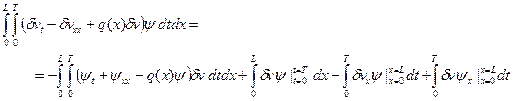
Имеем

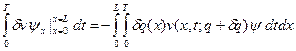
Тогда учитывая условия (13)-(15) и (17)-(19), получим, что

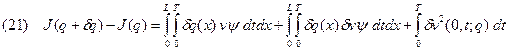
Последние два слагаемых в правой части равенства (21) имеют второй порядок малости. Тогда получаем следующий градиент функционала

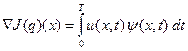
Здесь 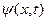- решение сопряженной задачи.