Численная реализация

Введем в области равномерную сетку по времени и пространству с шагами 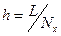, 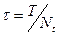. Индексы узлов: , .

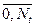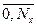Решаем прямую задачу (17)-(20) конечно-разностным методом.

При аппроксимации воспользуемся неявными схемами для уравнения теплопроводности. Уравнения на каждом шаге решаются методом прогонки.

Разностная схема для прямой задачи (24)-(27):

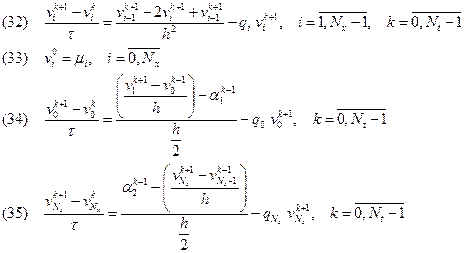
Разностная схема для сопряженной задачи (28)-(31):

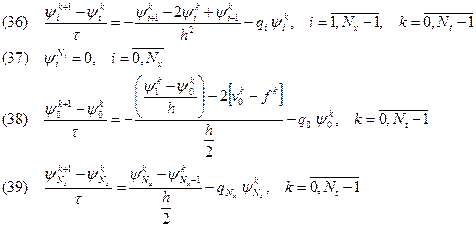
Выражение для градиента в случае кусочно-постоянного коэффициента:

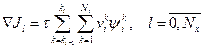
Здесь 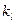- индекс точки разрыва коэффициента.