Связь между уравнениями

Рассмотрим, как от уравнения одного вида можно перейти к уравнению другого вида. Пусть

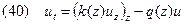
Предположим, что коэффициент 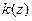имеет вид 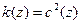. Тогда подставив 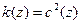в уравнение (40), перейдем к следующему уравнению

.

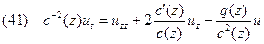Сделаем замену переменной в (41)

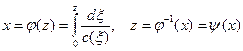
и введем новые функции

.

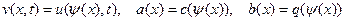Тогда получим следующее уравнение

.

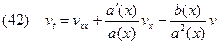Если ввести новые функции

,

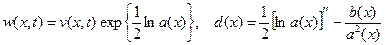тогда от уравнения (42) перейдем к уравнению

.

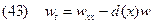Литература

1. Карслоу Г., Егер Д. Теплопроводность твердых тел. - М.: Наука, 1964.

2. Борисов Ю.П., Рябинина З.К., Воинов В.В., Особенности проектирования разработки нефтяных месторождений с учетом их неоднородности. - М.: Недра. 1976.

3. Желтов Ю.П., Стрижков И.Н. и др. Сборник задач по разработке нефтяных месторождений.- М.: Недра, 1985.

4. Баренблатт Г.И., Ентов В.М., Ряжик В.М. Теория нестационарной фильтраций жидкости и газа.- М.: Недра, 1972.

5. Марчук Г.И. Методы вычислительной математики. –3-е изд. – М.: Наука, 1989.

6. Самарский А.А., Гулин А.В. Численные методы. – М.: Наука, 1988.

7. Макаров В.Л., Хлобыстов В.В. Сплайн – аппроксимация функций. – М.: Высшая школа, 1983.

8. Самарский А.А. Теория разностных схем. – 2-е изд. – М.: Наука, 1983.

9. Тихонов А.Н., Самарский А.А. Уравнения математической физики. –
5-е изд. – М.: Наука, 1977.

10.Калиткин Н.Н. Численные методы. – М.: Наука, 1978.

11. Кабанихин С.И., Бектемесов М.А., Шишленин М.А. , Численные методы решения математических задач геофизики.-Алматы,2005 (интранет).

12. Владимиров Е.С. Уравнения математической физики. – М.: Наука, 1971.

Дополнительная литература

1. Н.В.Копченова, И.А.Марон. Вычислительная математика в примерах и задачах. – М.: Наука, 1972.

2. В.И.Дробышевич, В.П.Дымников, Г.С.Ривин. Задачи по вычислительной математике. – М.: Наука, 1980.

3. Куфуд, О. Зондирование методом сопротивлений. М.: Недра, 1980, 232 с.

4. Б.М.Будак, А.А. Самарский, А.Н.Тихонов. Сборник задач по математической физике.- М.: Наука, 1980.

5. Кошляков А.С., Глинпер Э.Б., Смирнов М.М. Дифференциальные уравнения математической физики. – М.: Наука, 1999.

6. Смирнов М.М. Задачи по уравнениям математической физики. М.: Наука, 2000.