Достоверность разности средних величин
На практике нередко приходится иметь дело не с одной, а с двумя средними: надо сравнить среднюю длительность пребывания больных в 2-х стационарах или за отчетный год и предыдущий, результаты, полученные при исследовании 2-х групп больных, лечившихся разными методами, исследуемую группу и контрольную и т.д. Целью сравнения двух средних является оценка существенности их различий, установление их достоверности.
Достоверность разности между двумя средними величинами определяется по формуле:
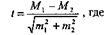
М 1 и М 2 — две средних арифметических величины, полученные в двух самостоятельных независимых группах наблюдений;
т 1 и т 2 — их средние ошибки (выражение 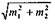 называют средней ошибкой разности двух средних);
называют средней ошибкой разности двух средних);
t — доверительный коэффициент для разности средних.
При t 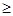 2 разность средних арифметических может быть признана существенной и неслучайной, то есть достоверной. Это значит, что и в генеральной совокупности средние величины отличаются, и что при повторении подобных наблюдений будут получены аналогичные различия. При t = 2 надежность такого вывода будет не меньше 95%. С увеличением t степень надежности также увеличивается, а риск ошибки уменьшается. При t < 2 достоверность разности средних величин считается недоказанной. Например, в больнице «А» средняя длительность пребывания больного на койке равна 16,2 дн., т =
2 разность средних арифметических может быть признана существенной и неслучайной, то есть достоверной. Это значит, что и в генеральной совокупности средние величины отличаются, и что при повторении подобных наблюдений будут получены аналогичные различия. При t = 2 надежность такого вывода будет не меньше 95%. С увеличением t степень надежности также увеличивается, а риск ошибки уменьшается. При t < 2 достоверность разности средних величин считается недоказанной. Например, в больнице «А» средняя длительность пребывания больного на койке равна 16,2 дн., т = 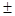 1,5 дн.; в больнице «В» — 14,8 и 1,0 соответственно.
1,5 дн.; в больнице «В» — 14,8 и 1,0 соответственно. 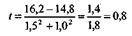
Различие средних арифметических недостоверно, статистически незначительно. Но нельзя в таких случаях говорить о том, что «нет разницы»! Различие есть, но оно может быть недостоверным.
В сопряженных совокупностях (зависимых рядах) оценка достоверности разности средних проводится по формуле:
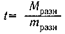
Дата добавления: 2015-01-29; просмотров: 1352;
