Оценка полученного результата по средней ошибке
| Доверительный коэффициент (критерий точности) | Спорность результата (достоверность) Pt | Риск ошибки Р |
| t1 =M± 1m | 68,3% (Pt- 0,683) | 0,317 |
| t2 = M±2m | 95,5% (Рt - 0,955) | 0,05 |
| t2,6 = M ± 2,6 m | 99,0% (Pt - 0,990) | 0,010 |
| t3= M ± 3 m | 99,7% (Pt- 0,997) | 0,003 |
| t3,3 = M ± 3,3 m | 99,9% (Рt - 0,999) | 0,001 |
В медико-статистических исследованиях обычно используют доверительную вероятность (надежность); равную 95,5 — 99,9%, а в наиболее ответственных случаях — 99,7%.
Таким образом, если δ является доверительной вероятностью появления необходимых данных в заданных границах, то является доверительным интервалом, с помощью которого определяются границы возможного размера изучаемого явления.
Зная размер ошибки, можно, как отмечалось выше, правильно определить требуемое число наблюдений для выборочного исследования при помощи преобразования формулы предельной ошибки выборки Δ (дельта) =
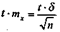, в которую входит величина п — число наблюдений.
Решая приведенное равенство относительно п, получим формулу для определения числа наблюдений:
Для примера воспользуемся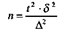 
данными изучения средней длительности пребывания больных в специализированном отделении. Здесь М = 20 дн., δ = ±1,63дн., m = +0,16 дн. Сколько же нужно дополнительно исследовать больных, заведомо оперируя ошибкой выборки больше полученной (Δ = ±0,5дн.), при доверительной вероятности t = 3.
Определяем требуемое число наблюдений:
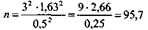
Вывод: для того, чтобы оперировать в использованном нами примере с указанной точностью (99,7%), следует подвергнуть изучению 95—96 больных. Нами исследовано 95 больных, что соответствует искомой величине.
Дата добавления: 2015-01-29; просмотров: 952;