Определение среднего роста 14-летних девочек
| Рост девочек в см, V | Центральная варианта группы, V | Число девочек, Р | V.-P |
| 133,0-136,9 137,0-140,9 141-144,9 145-148,9 153,0-156,9 157,0-160,9 161,0 – 164 165,0-168,9 | 133,0+137,0 ----------------- =135 137,0+141,0 ----------------- =139 ……………..=143 ……………..=147 ……………..=151 ……………..=155 ……………..=159 …………….=163 165,0+1697,0 ----------------- =167 | 135·3 = 405 ……….2085 ………..2431 ………...6027 …………7852 …………6510 …………2862 …………815 …………..668 |
n= 197 V1·Р= 29655

3. Если каждую варианту разделить или умножить на одно и то же число, то во столько же раз уменьшится или увеличится средняя арифметическая.
Эти свойства используют в тех случаях, когда варианты представлены очень малыми или, наоборот, большими числами.
В здравоохранении в отдельных случаях может потребоваться расчет средней прогрессивной. Средняя прогрессивная рассчитывается из лучших вариант, вариант, положительно характеризующих явление. Они могут иметь значение больше полученной средней арифметической (процент совпадения диагнозов, число больных, состоящих под диспансерным наблюдением, охват профилактическими осмотрами и т.д.) и меньше (уровень детальности, младенческой смертности, заболеваемости с временной нетрудоспособностью, частота послеоперационных осложнений и т.д.).
Вычисление средней прогрессивной длительности пребывания больных в терапевтических отделениях стационаров:
| Средняя длительность (в днях), V | Число стационаров, Р | V·P |
| n = 21 . |
М = 325/21 = 15,47 дней, но в 11 стационарах уровень средней длительности пребывания больных в стационаре ниже, то есть более благоприятный, чем в среднем по всем больницам. Рассчитанная в этих 11 стационарах новая средняя и будет средней прогрессивной: М = 155/11 = 14,09 дней. Такая средняя, определенная среди оптимальных условий, будет служить ориентиром для других (10) стационаров.
Средняя среди показателей. При одинаковых числах наблюдений ее можно рассчитать, как среднюю простую: то есть достаточно суммировать размеры показателей и затем поделить на их число. Но при разных числах наблюдений среднюю величину среди показателей следует определять всегда как среднюю взвешенную. Например, в трех отделениях стационаров летальность составила:
— хирургическое отделение — 1 %;
— терапевтическое отделение — 3%;
— неврологическое отделение — 5%.
Если суммировать показатели и разделить сумму на число отделений, то средний уровень летальности составит 3%. Однако в хирургическом отделении пролечилось 800 больных (умерло 8 человек), в терапевтическом 600 больных (умерло 18 больных), а в неврологическом пролечено 200 (умерло 10 больных). Таким образом, средняя летальность по больнице составляет 2,25 (36 · 100 : 1600). Разница оказалась заметной, чтобы определить средний показатель, надо узнать абсолютное число умерших в каждом отделении, получить сумму умерших, разделить ее на общую численность пролеченных больных и выразить полученную величину в соответствующих единицах (%, %о и т.д.).
Средняя величина абстрактна, она может быть рассчитана в принципе из любой совокупности, например, можно получать среднюю арифметическую в группе больных с повышенным и пониженным АД. Но такая средняя будет огульной, она не будет правильно характеризовать совокупность, из которой рассчитана. Средние необходимо рассчитывать из однородных совокупностей.
Средняя арифметическая величина находится в большой зависимости от колеблемости вариационного ряда, чем меньше колеблемость ряда, то есть, чем меньше амплитуда колебания ряда (разность между самой большой и самой малой вариантой, что называется степенью рассеяния ряда), тем более точно его будет характеризовать средняя арифметическая.
Если большинство вариант концентрируется около своей средней арифметической величину, то такой вариационный ряд — довольно компактный, однородный, можно говорить о малом варьировании. Если же варианта значительно удалена от своей средней арифметической - налицо большое варьирование, а возможно, и неоднородная совокупность.
Степень варьирования вариационного ряда определяется с помощью вычисления среднего квадратического отклонения (8). Для зачисления сигмы необходимо (см. табл. 5.8) определить отклонения (δ) каждой варианты от средней, возвести их в квадрат (α2), перемножить квадрат отклонения на частоту каждой варианты (α2р), получить сумму этих произведений ( 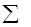 α2р), а затем вычислить сигму по формуле:
α2р), а затем вычислить сигму по формуле:
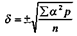
При малом числе наблюдений (n<30) расчет производят по следующей формуле:
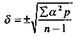
Описанный способ расчета среднего квадратического отклонения требует значительной вычислительной работы. Можно использовать приближенный способ вычисления среднего квадратического отклонения по амплитуде (размаху) вариационного ряда. Вычисление 5 по амплитуде производится по формуле:
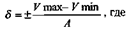
А — коэффициент для определения 5, соответствующий числу наблюдений (см. табл. 5.10).
В нашем примере (см. табл. 5.8) 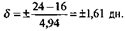
Для оценки варьирования признака наряду со средним квадратическим отклонением может быть использован коэффициент вариации (С). Особенно необходимо использовать коэффициент вариации при сравнении колеблемости двух или более средних величин, выраженных в разных единицах измерения: 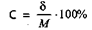
В нашем примере 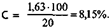
Значение коэффициента вариации менее 10% свидетельствует о малой колеблемости, от 10 до 20% о средней, от 20% и более — о сильной колеблемости вариант вокруг средней.
Значение среднего квадратического отклонения — δ.
1. δ характеризует однородность вариационного ряда. Если δ мала, значит ряд однородный, и рассчитанная М достаточно верно характеризует данный вариационный ряд. Если 6 велика, то ряд неоднородный, наблюдается большая колеблемость вариационного ряда, и полученная М характеризует не весь ряд, а только какую-то его часть.
2. В медицине, здравоохранении интервал М ± 1 δ обычно принимают за пределы нормы.
3. С помощью δ оценивается «выскакивающий» результат по формуле:
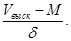 Если отношение разности между выделяющейся («выскакивающей») вариантой и средней арифметической, рассчитанной без нее, к среднему квадратическому отклонению, рассчитанному также без выделяющейся варианты, будет равно 3 и более, то такую варианту лучше не включать в исследование.
Если отношение разности между выделяющейся («выскакивающей») вариантой и средней арифметической, рассчитанной без нее, к среднему квадратическому отклонению, рассчитанному также без выделяющейся варианты, будет равно 3 и более, то такую варианту лучше не включать в исследование.
4. Теоретическое распределение вариант в однородном вариационном ряду подчиняется правилу трех сигм, которое графически изображается кривой Гаусса[7] (рис. 5.1).
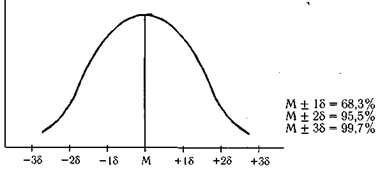
Рис. 5.1.Теоретическая кривая нормального распределения.
Если к средней арифметической величине прибавить и отнять от нее одну сигму (М ±15), то при нормальном распределении в этих пределах будет находиться не менее 68,3% всех вариант (наблюдений), что считается нормой для изучаемого явления. Если к 2 ± 28, то в этих пределах будет находиться 95,5% всех наблюдений, а если к М ± 38, то в этих пределах будет находиться 99,7% всех наблюдений. Таким образом, среднее квадратическое отклонение является стандартным отклонением, позволяющим предвидеть вероятность появления такого значения изучаемого признака, которое находится в пределах заданных границ.
Дата добавления: 2015-01-29; просмотров: 1289;
