Определение среднего срока пребывания больных в специализированном отделении больницы

Число дней, V	Число больных, Р	Произведения вариант на их частоты V • Р	Отклонения вариант от средней, d =V- м	Квадрат отклонений, d²	Произведение квадратов отклонений на частоты d²P
			-4 -3 -2 -1

n = 95 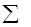= 1900

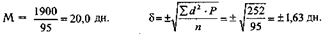
При большом количестве наблюдений число встречающихся размеров вариант может быть очень большим; тогда рекомендуется размеры вариант объединять в группы, причем каждая группа должна иметь равное число значений вариант (иметь равный интервал). Расчет средней арифметической в таком сгруппированном или интервальном ряду требует предварительного определения середины интервала. Середина интервала в непрерывных вариационных рядах определяется как полусумма первых значений соседних групп. Середина интервала в дискретных вариационных рядах определяется как полусумма крайних значений группы (табл. 5.9).

Средняя арифметическая имеет ряд свойств, которые используются в некоторых случаях для упрощения расчета средней.

1. Алгебраическая сумма отклонений всех вариант от средней равна нулю. На этом свойстве основан расчет средней по способу моментов.

2. Если к каждой варианте вариационного ряда прибавить или отнять одно и то же число, то на столько же увеличится или уменьшится средняя арифметическая величина.

Таблица 5.9

<34 35 363738 39 40 >

Дата добавления: 2015-01-29; просмотров: 880;