Достоверность показателей и разности показателей
Достоверность показателя определяется с помощью его средней ошибки по формуле: 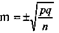 , где р - размер показателя, выраженный в долях единицы, в процентах, в промилле; q - равно 1 - р или 100 -р или 1000- р (величина, дополняющая показатель до основания); п — число наблюдений.
, где р - размер показателя, выраженный в долях единицы, в процентах, в промилле; q - равно 1 - р или 100 -р или 1000- р (величина, дополняющая показатель до основания); п — число наблюдений.
Например: обследовано 1800 больных, из них выявлено 90 больных гипертонической болезнью I ст. Процент выявленных больных по данным проведенного осмотра равен: 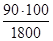 = 5 случаев на 100 осмотренных.
= 5 случаев на 100 осмотренных.
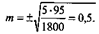
Следовательно, с вероятностью 95,5% показатель выявляемости больных с ГБ-1 в аналогичных условиях будет колебаться в пределах Р±2т = 5 ± 2 • 0,5 = 5± 1,0, то есть от 4 до 6 случаев на 100 обследованных.
Достоверность различий между сравниваемыми показателями вычисляется по формуле, аналогичной для средних величин:
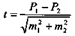
Оценивается критерий различия показателей так же, как и средних величин.
Для примера сопоставим уровни общей летальности в двух больницах:
| Больница № 1 | Больница №2 | |
| Число лечившихся | ||
| Из них умерло | ||
| Летальность | 4,5% (Р1) | 3,5% (Р2) |
Определим средние ошибки показателей:
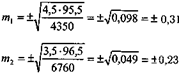
Вычисляем критерий различия:
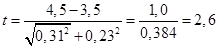
Рассчитанный критерий различия равен 2,6, то есть больше 2, что указывает на достоверною, не случайную, статистически значимую разницу уровней летальности в сравниваемых больницах.
Оценка нулевого эффекта. При альтернативном распределении (либо-либо), когда показатель равен нулю (Р = 0) или близок к нулю, a q = 100% или когда показатель равен 100% (Р = 100%) или близок к 100%, a q = 0, следует узнать, а каким бы мог быть показатель изучаемого явления при других условиях отбора (другое число наблюдений, другой состав больных по полувозрасту и т.д.)? Для этого пользуются специальной формулой, по которой можно вычислить, «ожидаемый» уровень показателя:
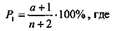
а — результативный показатель (Р).
Допустим, что в больнице лечилось экспериментальным методом 60 больных (п), среди которых летальных исходов не было (P=0%). Вычисляем «ожидаемый» показатель летальности:
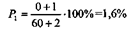
Ошибка такого показателя определяется по формуле: 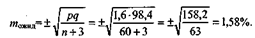
При t = 2 возможны колебания ожидаемого показателя в пределах от 0% до 4,78% (1,6 ±3,18).
Дата добавления: 2015-01-29; просмотров: 2520;
