Схема оценки тесноты корреляционной связи по коэффициенту корреляции
| Теснота связи | Величина коэффициента корреляции при наличии | |
| прямой связи ( + ) | обратной связи ( — ) | |
| Связь отсутствует Связь слабая Связь умеренная Связь сильная Связь полная (функциональная) | от 0 до +0,3 от +0,3 до +0,7 от +0,7 до +1,0 + 1,0 | 0 от 0 до —0,3 от -0,3 до -0,7 от -0,7 до -1,0 - 1,0 |
Приведем пример вычисления коэффициента корреляции по приведенной формуле (см. табл. 5.15).
• Ход вычислений здесь чрезвычайно прост. Суммируя ряды х и у, получаем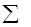 
х = 119 и 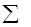у = 105,2. Деля суммы на число членов ряда (п), получаем средние арифметические этих рядов: Мх = 119: 12 = 9,9 и Мх = 105 : 12 = 8,8. Ряды dx и dy, то есть отклонение чисел рядов х и у представляют собой разность между соответствующими значениями х и у и средним арифметическим этих рядов. Так, для ряда х, dx равно для января: х-М = 5-9,9 = -4,9; для февраля: х-М = 2-9,9 = -7,9 и т.д. Возводя поочередно числа рядов dx и dy в квадрат, получаем ряды 
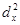и 
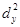,aпреумножая попарно числа рядов dx и dy между собой, получаем ряд dx • dy.
Таблица 5.15
Дата добавления: 2015-01-29; просмотров: 932;