Непараметрические критерии
Непараметрические критерии используются преимущественно в тех случаях, когда изучаемое явление отличается от нормального распределения. С одной стороны, они позволяют оценить характер, тенденцию явления (увеличение, уменьшение, без перемен), хотя, с другой, большинство из них обладает достоверно высокой статистической мощностью (чувствительностью). Особенно эффективно применение непараметрических критериев при малых выборках (п<30), при изучении качественных признаков. Преимуществом большинства непараметрических критериев является сравнительная простота расчетов.
Основные направления применения непараметрических критериев:
1. Для характеристики одной совокупности:
— критерий итераций (флуктуации);
— медиана, квартели.
2. Для оценки связи между явлениями:
— коэффициент ранговой корреляции (Спирмена);
— коэффициент корреляции рангов (Кэндела);
— показатель соответствия χ2 (хи-квадрат)..
3. Для оценки различий двух сравниваемых совокупностей. При этом следует выделять несколько вариантов:
1. Для сравнения количественных признаков:
| Две выборки | Несколько выборок | ||
| А | Б | В | Г |
| независимые | зависимые | независимые | зависимые |
Критерий Лорда ( 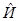 ) Критерий Вилкоксона— Манна-Уитни(И) Критерий Мостселлера ) Критерий Вилкоксона— Манна-Уитни(И) Критерий Мостселлера
| Ранговый критерий Вилкоксона (Т) Критерий знаков (Z) | Сравнение выборок по Немени | Критерий Фридмана Критерий Вилкоксона |
| Критерий Розенбаума (Q) Критерий Уайта (К) Серийный критерий Вальда— Вольровича (S) Критерий Колмогорова -Смирнова (λ) | Максимум критерий для разности пар |
2. Для сравнения качественных признаков:
| Две выборки | Несколько выборок . | ||
| Д | Е | Ж | |
| независимые | зависимые | независимые | зависимые |
| Критерий Стьюдента с поправками Йетса Критерий согласия (χ2 ) | Критерий Макни— Мара | Критерий (χ2) по Р.Руниони | Критерий Кокрена (Q) |
| Точный метод Фишера (χ2) Критерий Ван— дер— Вардена (X) |
Конкретные не параметрические критерии подробно изложены в специальных руководствах по медицинской статистике.
Дата добавления: 2015-01-29; просмотров: 1992;
