Алгебраический и фундаментальный критерии устойчивости

C математической точки зрения свойство устойчивости можно трактовать следующим образом..

Ранее было показано, что поведение любого усилительного устройства с заданной степенью точности можно описать дифференциальным уравнением. Если известно решение этого уравнения для входного воздействия произвольного вида, то известно и поведение усилителя во всех условиях его работы, т. е. при произвольных возмущающих воздействиях. Решение данного уравнения можно рассматривать как некоторую траекторию движения в пространстве параметров усилительного устройства:

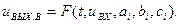(2.2.8)

Это так называемое невозмущенное движение системы.

Естественно, если на усилительное устройство действует некоторое внешнее возмущение в виде напряжения 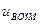, то его поведение

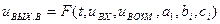(2.2.9)

будет отличаться от описываемого выражения(2.2.8).

Выражение для возмущенного движения 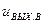также описывает некоторую траекторию движения в пространстве параметров устройства.

Отличие возмущенного и невозмущенного движений устройства

описываемое функцией вида:

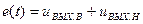(2.2.10)

и используется для математического определения понятия устойчивости системы. В смысле функции e(t) невозмущенному движению системы соответствует точка начала координат пространства параметров усилителя.

Свойства устойчивости системы обычно определяется по виду функции e(t), возникающей при кратковременном воздействии на усилительное устройство какого-либо внешнего возмущения.

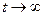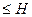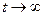Говорят, что усилительное устройство устойчиво, если для любых отклонений его параметров или внешних возмущений, действующих в момент t₀ и вызывающих отклонение e(t0), лежащее в некоторой конечной области S₀, величина e(t) при не превысит некоторого заданного значения Н, т. е. максимум e(t) , при . Геометрическая интерпретация данного условия показана на рис. 2.2.5.а.

Если сформулированное условие не выполняется, говорят, что устройство неустойчиво.

На практике часто пользуются понятием асимптотической устойчивости. Для этого случая выполняется условие:

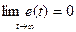. (2.2.11)

Физически это означает, что после окончания внешнего возмущающего воздействия выходной параметр устройства вернется к своему первоначальному, невозмущенному значению.