Частотный критерий устойчивости

Устойчивость является обязательным условием функционирования любого усилительного устройства, без соблюдения которого оно не может выполнять возлагаемые на него функции. В физическом понимании свойство устойчивости означает, что конечные изменения входного сигнала или действие небольших, наперед заданных значений внешних возмущений, или ограниченные изменения самих параметров устройства не приводят к значительным, неограниченным, применительно к данному устройству, отклонениям выходного сигнала. Эти неограниченные отклонения выходного сигнала могут выражаться в увеличении или уменьшении выходного сигнала устройства до максимально или минимально возможного значения, появлении на выходе установившихся периодических колебаний, частота которых не связана с параметрами входного сигнала и т.п.

Следует отметить, что свойство устойчивости относится к усилительному устройству, содержащему цепь ОС. Это может быть либо внутренняя связь, обусловленная физическими свойствами и выполнением элементов устройства, либо паразитная связь (емкостная или индуктивная), обусловленная конструктивными особенностями его изготовления, либо внешняя ОС, выполненная путем введения в устройство специальных цепей. Если подобная связь отсутствует, то усилительное устройство является разомкнутым понятие устойчивости к нему не применимо.

Использование такого подхода всегда позволяет однозначно ответить на вопрос устойчивости исследуемого устройства. Однако на практике непосредственное отыскание точных решений уравнения (2.2.1) является трудоемкой задачей. Поэтому для решения вопроса устойчивости усилительного устройства удобнее пользоваться некоторыми косвенными оценками, позволяющими ответить на поставленный вопрос без решения дифференциальных уравнений.

Такие оценки, называемые критериями устойчивости, могут быть получены на основе рассмотрения амплитудно-фазовых характеристик устройства. Наиболее известным из них является критерий устойчивости Найквиста, который позволяет судить об устойчивости по виду амплитудно-фазовых характеристик разомкнутого контура регулирования системы. Он формулируется следующим образом.

Если разомкнутое (в смысле цепи внешней ОС) усилительное устройство устойчиво и его амплитудно-фазовая характеристика при изменении частоты от 0 до 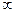не охватывает точку с координатами ( 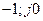), то после замыкания цепи ООС устройство будет также устойчиво.

Прохождение годографа через точку с координатами ( 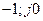) означает нахождение усилителя на границе устойчивости.

На рис. 2.2.5 б приведены примеры амплитудно-фазовых характеристик, удовлетворяющих сформулированному выше условию. Характеристика 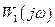соответствует абсолютно устойчивой системе. Вывести ее из устойчивого режима работы можно только путем увеличения коэффициента усиления. Характеристика 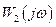соответствует условно устойчивой системе. В этом случае потеря устойчивости возможна как при увеличении, так и при уменьшении коэффициента усиления.

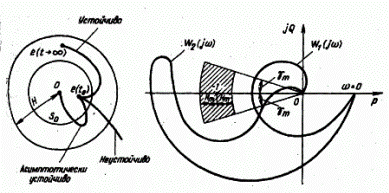
а) б)

Рис. 2.2.5. а - геометрическая интерпретация устойчивости усилителя; б - годографы устойчивого усилительного устройства.

Введем понятие запаса устойчивости. Считают, что усилитель обладает запасом устойчивости, если он удовлетворяет условиям устойчивости при значениях модуля 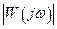, отличающихся от 1 не менее, чем на некоторую наперед заданную величину 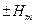, называемую запасом устойчивости по модулю, и имеет фазовый угол, отличающийся от я не менее, чем на величину 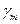, называемую запасом устойчивости по фазе. Согласно данному определению (для обеспечения заданного запаса устойчивости) амплитудно-фазовая характеристика усилителя не должна попадать в область, заштрихованную на рис. 2.2.5, б.

При проектировании усилителей удобнее пользоваться не амплитудно-фазовыми, а его логарифмическими амплитудной и фазовой характеристиками. Сформулированные выше условия легко можно распространить и на эти характеристики. Логарифмическая амплитудная и фазовая частотная характеристики, соответствующие амплитудно-фазовой характеристике 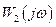(рис. 2.2.5, б), показаны на рис. 2.2.6.

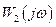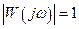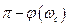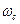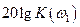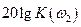Легко показать, что точка пересечения ЛАЧХ с осью частот соответствует точке пересечения годографа с окружностью единичного радиуса, то есть соответствует значению . Тогда значение фазового угла , соответствующее частоте , является запасом по фазе, и значения и , соответствующие пересечению фазовой характеристики с уровнем 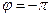, являются соответствующими запасами по модулю. Для получения требуемых запасов устойчивости по модулю и фазе для логарифмических характеристик необходимо выполнение следующих условий:

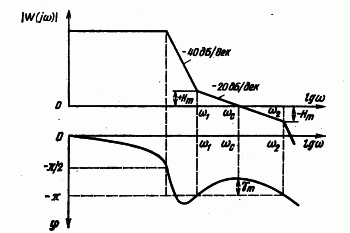
Рис. 2.2.6. ЛАЧХ и ФЧХ устойчивого усилительного устройства, соответствующие годографу .

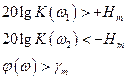. (2.2.7)

Следовательно, при заданных запасах устойчивости по модулю и фазе на логарифмических амплитудной и фазовой характеристиках всегда можно определить области, в которые эти характеристики не должны заходить. Следовательно вопрос устойчивости решается без нахождения точного решения исходной системы дифференциальных уравнений путем соответствующего выбора вида логарифмических характеристик.