Способ итераций решения СЛАУ
При большем числе неизвестных линейной системы схема Гаусса, с помощью которой осуществляют методически точные решения, становится весьма сложной. В этих случаях для нахождения корней системы удобнее применять приближенные численные способы. Одним из таких способов является способ итераций.
Пусть дана линейная система
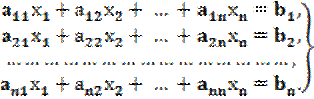(2.18)
Представим систему (2.18) в матричном виде, введя соответствующие матрицы
А =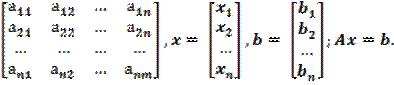 
(2.19)
Предполагая, что диагональные коэффициенты не равны 0 (аij ≠ 0, i = 1, 2 ,…, n), разрешим первое уравнение (2.18) относительно x1, второе - относительно х2 и т. д. Тогда получим эквивалентную систему
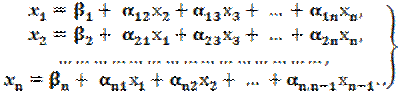(2.20)
где βi =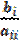 
; аii = – 
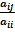при i ≠ j. Вводя матрицы αij = 0 при i = j
α =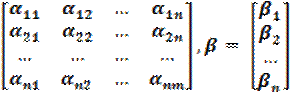 
,
систему (2.20) можно записать в матричной форме:
х = β + αх (2.21)
Эту систему можно решать методом последовательных приближений. За нулевое приближение можно принять столбец свободных членов х(0) = β.
Далее находим первое приближение в виде матрицы-столбца х(1) = β + αх(0), затем второе приближение х(2) = β + αх(1) и т. д. Любое (к+1)-е приближение вычисляют по формуле
х(k+1) = β + αх(k), k = 0,1, 2 ,…(2.22)
Если последовательность приближений x(0), x(1), …, x(k),… имеет предел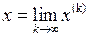 
, то этот предел является решением системы (2.20).
Процесс итераций хорошо сходится, если элементы матрицы α малы по абсолютной величине. Иными словами, для успешного применения способа итераций модули диагональных коэффициентов системы (2.18) должны быть велики по сравнению с модулями диагональных коэффициентов этой системы (свободные члены роли не играют).
Пример. Решить систему способом итераций
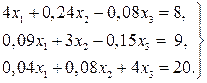
В данной системе диагональные коэффициенты значительно преобладают над остальными коэффициентами при неизвестных.
Приведем эту систему к виду (2.20):
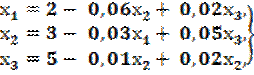. (2.23)
В матричной форме эту систему можно записать так:
.
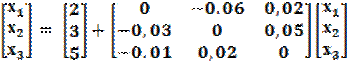За нулевые приближения корней системы (2.20), примем свободные члены, т.е.
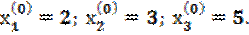
Подставляя эти значения в правые части уравнений (2.23), получим первые приближения корней:
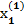= 2 – 0,06 · 3 + 0,02 · 5 = 1,92;
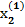= 3 – 0,03 · 2 + 0,05 · 5 = 3,19;
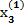= 5 – 0,01 · 2 + 0,02 · 3 = 5,04.
Далее, подставляя первые приближения в систему (2.23), получим вторые приближения корней
;
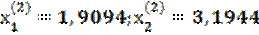После новой подстановки будем иметь третьи приближения корней:
; 
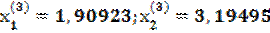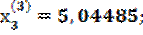и т.д.
На этом процесс нахождения корней можно закончить.
Проведя округление до второго десятичного знака, получим корни с абсолютной погрешностью менее 0,005;
; 
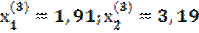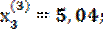и т.д.
Дата добавления: 2015-02-03; просмотров: 879;