Решение систем линейных уравнений способом Гаусса
Способ Гаусса является одним из наиболее распространенных способов решения систем линейных уравнений. Если точно выполнить все необходимые действия, то мы получим точное решение системы. В этом смысле способ Гаусса называют точным.
Практически, поскольку арифметические действия приходится выполнять с округлением, точного решения получить не удается.
В основе способа Гаусса лежит идея последовательного исключения неизвестных. Вычислительные схемы реализации этого способа могут быть различны. Мы рассмотрим одну из них – схему единственного деления.
Для удобства изложения ограничимся рассмотрением примера конкретной системы четвертого порядка. Те же приемы используются и в случае большего числа уравнений в системе:
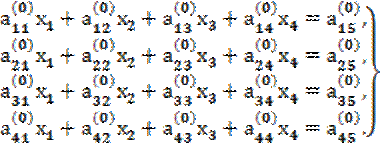 (2.9)
(2.9)
Предположим, что коэффициент 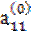 , называемый ведущим элементом первой строки, не равен нулю. Разделив первое из уравнений (2.6) на
, называемый ведущим элементом первой строки, не равен нулю. Разделив первое из уравнений (2.6) на 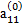 , получим:
, получим:
х1 + 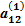 х2 +
х2 + 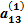 х3 +
х3 + 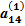 х4 =
х4 = 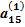 , (2.10)
, (2.10)
где 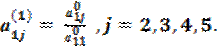
Исключим х1, вычитая из каждого уравнения системы (2.9), начиная со второго, уравнение (2.10), умноженное на коэффициент при x1, в соответствующем уравнении. В результате получим
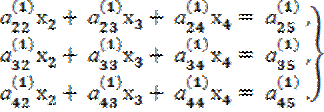 (2.11)
(2.11)
где 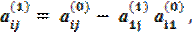 i = 2,3,4; j = 2,3,4,5.
i = 2,3,4; j = 2,3,4,5.
Допустим, что ведущим является элемент второй строки 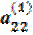 ≠ 0. Тогда, разделив на него члены первого из уравнения (2.11), получим уравнение
≠ 0. Тогда, разделив на него члены первого из уравнения (2.11), получим уравнение
х2 + 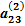 х3 +
х3 + 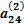 х4 =
х4 = 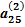 ,(2.12)
,(2.12)
где 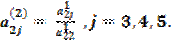
Исключив с помощью уравнения (2.12) неизвестную величину х2 из двух последних уравнений (2.11), приходим к уравнениям вида
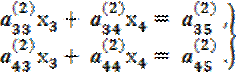 (2.13)
(2.13)
где 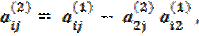 i = 3,4; j = 3,4,5.
i = 3,4; j = 3,4,5.
Если ведущим является элемент третьей строки 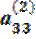 ≠ 0, то, поделив на него члены первого из уравнений (2.13) и вычтя найденное уравнение, умноженное на
≠ 0, то, поделив на него члены первого из уравнений (2.13) и вычтя найденное уравнение, умноженное на 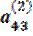 из второго уравнения, получим
из второго уравнения, получим
х3 + 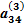 х4 =
х4 = 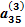 , (2.14)
, (2.14)
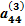 х4 =
х4 = 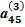 , (2.15)
, (2.15)
где 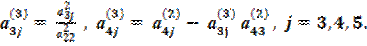
Наконец, если элемент 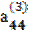 ≠ 0, то, разделив на него уравнение (2.15), приведем его к виду
≠ 0, то, разделив на него уравнение (2.15), приведем его к виду
х4 = 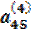 , (2.16)
, (2.16)
где 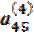 =
= 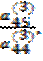
Итак, мы получим систему с треугольной матрицей, эквивалентной системе (2.9)
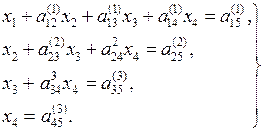 (2.17)
(2.17)
Эта система получена путем объединения уравнений (2.10), (2.12), (2.14) и (2.16). Процесс приведения системы (2.9) к треугольному виду (2.17) называется прямым ходом, а нахождение неизвестных из системы (2.17) – обратным ходом.
Решение системы уравнений по способу Гаусса удобно производить, занося все вычисления в табл. 2.3
Таблица 2.3
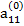
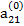
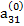
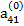
| 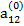
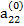
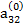
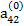
| 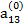
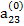
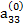
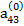
| 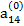
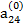
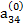
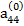
| 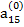
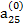
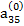
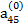
|
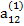
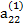
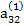
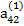
| 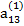
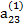
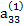
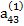
| 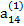
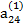
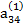
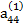
| 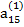
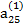
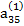
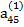
| |
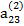
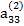
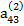
| 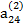
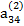
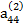
| 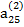
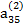
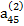
|
| . . . | . . . | 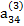
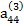
| 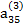
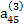
| |
| . . . | . . . | . . . | х4 | |
| . . . | . . . | … | х3 | |
| . . . | … | … | х2 | |
| … | … | … | х1 |
В табл. (2.3) единицами, расположенными в соответствующих диагоналях, указываются строки с коэффициентами, соответствующими выражениям (2.17), по которым определяются неизвестные хi. Кроме того, элемент 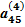 опущен, так как он совпадает с х4.
опущен, так как он совпадает с х4.
Дата добавления: 2015-02-03; просмотров: 1018;
