Закон постоянства углов кристалла. Формула Вульфа-Брэгга.

Когда образуется кристалл, частицы выстраиваются в закономерные симметричные ряды сетки решетки. Грани образующих их кристаллических многогранников соответствуют плоскостям, составленным из материальных частиц, а ребра кристалла – линиям пересечения этих плоскостей. Очевидно, любой ряд в структуре соответствует возможному ребру кристалла, а любая плоскость – возможной грани кристалла. Грани образуются параллельными самим себе.

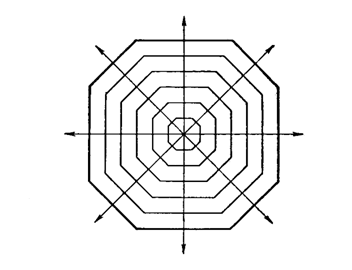
Рисунок 5. Схема параллельного нарастания граней кристалла.

Стрелками изображены нормали к граням.

Н. Стенон в 1669 году открыл закон постоянства углов: во всех кристаллах данного вещества, при одинаковых условиях, углы между соответствующими гранями кристаллов постоянны.

Кристаллы разных веществ отличаются друг от друга внешней формой, у кристаллов одного и того же вещества внешний облик (габитус) может оказаться совсем различным, но углы между соответствующими гранями останутся постоянными.

Закон постоянства углов позволяет свести все многообразие пространственных многогранников к совокупности углов между гранями и изобразить их с помощью проекции.

Этот закон сыграл огромную роль в развитии кристаллографии. До открытия отражений рентгеновских лучей кристаллы характеризовались и отличались друг от друга только по углам между их гранями.

Основным методом диагностики в кристаллографии стало измерение углов в кристалле между гранями на ренгенгониометре (отраженный или преломляющий). Схема дифракции рентгеновских лучей атомными плоскостями дана на рисунке 6.

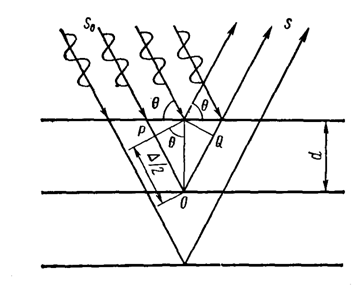
Рисунок 6. К выводу условия Вульфа-Брэгга.

Из схемы видно разность хода между падающими и отраженными лучами равна

D=PO+OQ=2PQ=2dsinq

Если D=nl, где n=1,2,3…., l - длина волны рентгеновского излучения (l=0,154 нм), то наблюдается максимум интенсивности отраженных лучей. 2dsinq=nl (n=1,2,3…) Равенство выражает закон Вульфа—Брэгга, открытый в 1913г.

Угол падения q дает максимальное отражение не при любом значении, а при тех, когда выполняется условие Брэгга. Этот угол обозначается q_Б.

Для каждого кристалла и для каждой грани этот угол имеет определенное значение. Для известных кристаллов эти значения приведены в соответствующих кристаллографических таблицах.

Измерение производится с помощью рентгеновского гониометра, принцип работы которого аналогичен гониометру, работает на отражение, только вместо источника света применяется рентгеновская вакуумная трубка, источник рентгеновского излучения, а в качестве приемника излучения применяется детектор, аналогичный камере Вильсона, счетчику Гейгера или сцинтилляционный оптический датчик.

С помощью него можно измерить межатомное расстояние a

Метод кристаллографического индицирования атомных плоскостей.

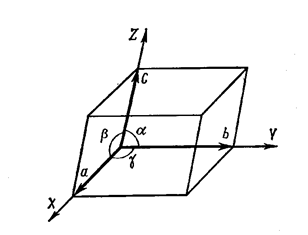Кристаллическая решетка характеризуется шестью параметрами элементами ячейки: длинами ребер a,b,c и углами a,b,g

В общем случае:

a≠b≠c

a≠b≠g

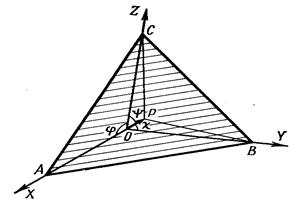
Рисунок 7.Элементарный параллелепипед.

Для описания кристаллических многогранниковых структур применяется метод кристаллографического индицирования, удобный для всех кристаллографических систем, независимо от того прямоугольные они или косоугольные, одинаковые у них отрезки или разные.

Расстояние в кристаллах будем измерять в длинах ребер a,b,c. Тогда

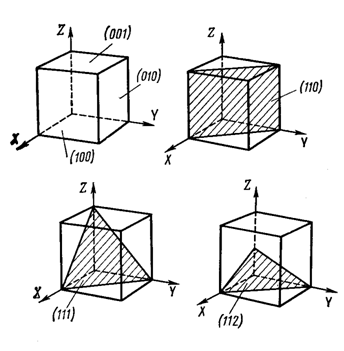
Рисунок 8. Символы некоторых плоскостей в кубической решетке

1. Плоскость или грань, перпендикулярная оси х, записывается (100)

2. Плоскость или грань, перпендикулярная оси у, записывается (010)

3. Плоскость или грань, перпендикулярная оси z, записывается (001)

Для грани перпендикулярной оси х; (hkl)=(100): h=1, k=0, l=0

hkl- атомная плоскость

a/h;b/k;c/l – отрезки, отсекаем плоскостью hkl на осях координат x,y,z

h,k,l- простые целые числа

hkl

c/l

a/h

b/k

Рисунок 9. Индексы Миллера для плоскостей hkl

Обозначение (hkl) носит название индексов Миллера. Они показывают сколько раз плоскость данного типа пересекает оси кристалла в данной элементарной ячейке.

Наряду с обозначениями кристаллографических плоскостей в круглых скобках задается направление перпендикулярное к этим плоскостям.

Индексы этого перпендикулярного направления такие, как у плоскости <hkl>,[hkl].

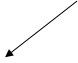
Символы некоторых направлений в плоской сетке и осей координат.

Все направления в кристалле равнозначны. Тогда направления ряда определяются двумя точками: началом координат и любым узлом ряда символ ряда пишут в квадратных скобках [mpn] (Рисунок 10).

Рисунок 10. Символы некоторых направлений в плоской сетке (а) и осей координат (б)

Главное преимущество такой индексации: символы осей координат не зависят от углов между осями координат и от осевых отрезков, они одинаковы в любой системе координат.