Алгоритм отделения корней методом последовательного перебора
Сущность метода.Большая производительность современных ЭВМ дает возможность отделить все действительные корни уравнения методом последовательного перебора. Нижнюю границу А и верхнюю границу В корней уравнения выбирают приблизительно, исходя из физического содержания задачи, описываемой решаемым уравнением, или из графика функции у= F(х). В основе этого метода лежит теорема 1: выбирается начальное значение х = А, затем с фиксированным шагом 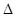 х = Н вычисляются значения функции F в точках А+kН (k = 0), 1, 2,...) до тех пор, пока она не изменит знак. Пусть, например, после n-го шага в точке х = А+nН функция F сменила знак, тогда [А+(n--1)Н; А+nН] - отрезок изоляции корня, P=А + nH -
х = Н вычисляются значения функции F в точках А+kН (k = 0), 1, 2,...) до тех пор, пока она не изменит знак. Пусть, например, после n-го шага в точке х = А+nН функция F сменила знак, тогда [А+(n--1)Н; А+nН] - отрезок изоляции корня, P=А + nH - 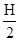 - приближенное значение корня уравнения с точностью e =
- приближенное значение корня уравнения с точностью e = 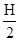 , то есть |x - P| £
, то есть |x - P| £ 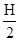 . Правый конец этого отрезка принимают за начальное значение следующего корня, если он есть. Такое продвижение вправо по оси Ох продолжают до тех пор, пока не достигнут верхней границы корней В. Этот алгоритм последовательного перебора требует большого объема вычислительной работы, обусловленного многократным вычислением значения функции F с шагом Н. Естественно, что для ручных вычислений он непригоден. Основной проблемой является выбор шага.
. Правый конец этого отрезка принимают за начальное значение следующего корня, если он есть. Такое продвижение вправо по оси Ох продолжают до тех пор, пока не достигнут верхней границы корней В. Этот алгоритм последовательного перебора требует большого объема вычислительной работы, обусловленного многократным вычислением значения функции F с шагом Н. Естественно, что для ручных вычислений он непригоден. Основной проблемой является выбор шага.
Цель алгоритма - отделить корни и найти их грубые приближенные значения. Следует отметить, что метод последовательного перебора не дает полной гарантии, что ни один из корней уравнения не будет потерян, особенно в тех случаях, когда корни достаточно близки друг к другу, а шаг не слишком мал. В таких случаях надо произвести новый просчет с более мелким шагом Н.
Дата добавления: 2015-03-11; просмотров: 1794;
