Точные и приближенные методы решения линейных уравнений
3.1 Алгоритм отделения корней уравнения (аналитический метод)
Алгоритм отделения корней уравнения F(х)=0 должен предусматривать выполнение таких указаний:
1. Найти область определения уравнения - множество всех значений аргумента, при которых определены функции, составляющие уравнение.
2. Вычислить F'(х) и найти критические точки.
3. 3аписать интервалы монотонности.
4. Исследовать знак функции на концах интервалов монотонности.
5. Выписать отрезки изоляции корней.
6. Полученные отрезки изоляции корней сузить каким-либо методом.
При написании алгоритмов предполагается, что все указания алгоритма выполняются последовательно друг за другом в порядке их написания, если не оговорена иная последовательность.
Пример 1. Отделить корни уравнения F (х)=х 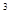 -4х
-4х 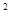 +2=0.
+2=0.
1.Х= (-¥, ¥)
2.F'(х)=3х 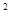 -8х; Зх
-8х; Зх 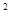 -8х=0.
-8х=0.
Критические точки: 0; 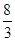 .
.
3.Интервалы монотонности: (-¥; 0),(0; 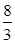 ),(
),( 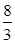 ;+¥)
;+¥)
4.Исследование знака функции на концах интервалов
монотонности дает: lim F(x)= - 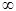 , F(0) 2, F
, F(0) 2, F 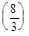 = -
= - 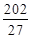 , lim F(х)= +
, lim F(х)= + 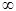
5.Отрезки изоляции корней: (-¥; 0),(0; 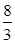 ),(
),( 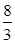 ;+¥)
;+¥)
6.Методом проб сузим полученные интервалы до единичной длины:
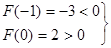 Þ[-1; 0]
Þ[-1; 0]
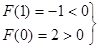 Þ[0; 1]
Þ[0; 1]
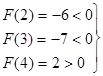 Þ[3; 4]
Þ[3; 4]
Таким образом, данное уравнение имеет три действительных корня, причем
-1< x 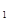 < 0;
< 0;
0< x 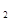 < 1;
< 1;
3< х 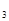 < 4.
< 4.
Левые концы отрезков изоляции корней можно принять за приближенные значения корней с недостатком, правые - с избытком.
Дата добавления: 2015-03-11; просмотров: 1407;
