Точные и приближенные методы решения систем линейных уравнений
Самое простое уравнение — это линейное уравнение с одной переменной х вида:
ах = b. (1)
Обобщением таких уравнений является линейное уравнение с несколькими переменными х1, х2, ..., хn вида:
a1x1 + a2x2 +...+ anxn = b. (2)
Многие задачи сводятся к решению конечного множества уравнений вида (2), то есть системы линейных уравнений. В общем виде система n линейных уравнений с n переменными x1, x2,..., xn записывается как совокупность числовых равенств:
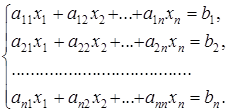 (3)
(3)
Коэффициенты aij системы для их упорядочения снабжаются двумя индексами, причем индекс i соответствует номеру строки, а j —номеру столбца (i = 1, 2,..., n; j = 1, 2,..., n). Тогда свободный член запишется в виде bi(i = 1, 2,..., n), а переменная— хj (j = 1, 2,..., n). Будем далее считать, что упорядоченные наборы чисел aij, xj и bi берутся из множества действительных чисел R. Решением системы (3) n уравнений с n переменными называют упорядоченную совокупность n чисел c1, c2, ...,cn 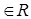 . являющуюся решением каждого из уравнений, входящих в систему. Ясно, что эта совокупность чисел при подстановке ее в систему (3) вместо х1, х2, ..., хn обращает каждое уравнение системы в истинное числовое равенство. Таким образом, множество решений системы является пересечением множеств решений, входящих в систему уравнений.
. являющуюся решением каждого из уравнений, входящих в систему. Ясно, что эта совокупность чисел при подстановке ее в систему (3) вместо х1, х2, ..., хn обращает каждое уравнение системы в истинное числовое равенство. Таким образом, множество решений системы является пересечением множеств решений, входящих в систему уравнений.
В частном случае, при n = 2 и n = 3 получаем хорошо знакомые системы двух линейных уравнений с двумя переменными:
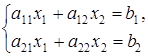 (4)
(4)
и трех линейных уравнений с тремя переменными:
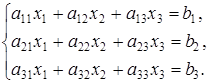 (5)
(5)
Решением системы (4) является упорядоченная пара чисел (c1, c2), а решением системы (5) — упорядоченная тройка чисел (с1, c2, c3).
Известно, что исследование и нахождение решения для систем (4) и (5) не представляют особых трудностей. Но задачи практического содержания сводятся к исследованию и решению систем линейных уравнений, содержащих десятки, сотни и даже тысячи переменных. Число элементарных операций при решении линейных систем с n переменными пропорционально примерно n3, поэтому решение таких задач стало возможным только с появлением быстродействующих ЭВМ.
Не останавливаясь на вопросах исследования систем линейных уравнений, в дальнейшем будем предполагать, что система имеет единственное решение. Поэтому основной задачей этой главы и будет изучение универсальных вычислительных алгоритмов, используемых для нахождения единственного решения системы линейных уравнений, когда число переменных совпадает с числом уравнений.
Методы решения систем линейных уравнений можно разделить на две группы: точные и итерационные (приближенные) методы.
Точными являются такие методы, которые позволяют получить решение системы после выполнения конечного числа арифметических операций над коэффициентами системы и их свободными членами. Причем решение получится точным только тогда, когда коэффициенты и правые части системы (3) известны точно и все арифметические действия над ними выполняются без округлений. Из точных методов рассмотрим метод Гаусса и правило Крамера. Однако на практике даже этими методами не всегда удается получить точное решение, ибо в ЭВМ точные коэффициенты представляются приближенно с некоторой погрешностью, а в процессе вычислений необходимо проводить округление чисел.
Итерационными являются методы, позволяющие получать решение системы с заданной точностью путем сходящихся бесконечных процессов. Из приближенных методов рассмотрим ниже метод итераций.
4.1 Алгоритм метода Гаусса
Пусть дана система n линейных уравнений с n переменными:
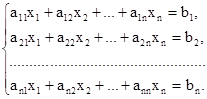
Коэффициенты аij при переменных будем рассматривать как элементы двумерного массива A (N, N), а свободные члены bi— как элементы одномерного массива В (N). Решение xi(i = 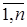 ) разместим в одномерном массиве В (N). Коэффициенты аij и свободные члены bi будем рассматривать как элементы расширенной матрицы
) разместим в одномерном массиве В (N). Коэффициенты аij и свободные члены bi будем рассматривать как элементы расширенной матрицы
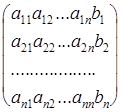 .
.
Предписываемые методом Гаусса преобразования будем выполнять над элементами расширенной матрицы. Опишем формально алгоритм решения линейной системы методом Гаусса без выбора главного элемента.
1. Элементы первой строки расширенной матрицы (А | В)делим на а11. Полученную после такого деления первую строку умножаем последовательно на ak1(k = 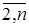 ) и вычитаем ее затем из k-ой строки (k =
) и вычитаем ее затем из k-ой строки (k = 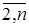 ). После этого преобразования в первом столбце массива A (кроме
). После этого преобразования в первом столбце массива A (кроме 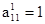 ) все элементы будут равны нулю, то есть получим матрицу:
) все элементы будут равны нулю, то есть получим матрицу:

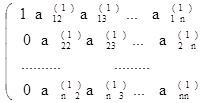
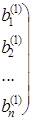
2. Элементы второй строки расширенной матрицы делим на 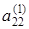 , затем умножаем ее последовательно на
, затем умножаем ее последовательно на 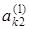 и вычитаем из оставшихся строк при
и вычитаем из оставшихся строк при 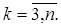
3. Продолжаем этот процесс исключения переменных (получения нулей) до тех пор, пока подобная процедура не будет проделана с (n — 1)-й строкой матрицы. После этого получим матрицу:

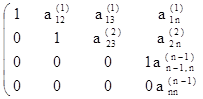
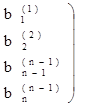
4. Элементы n-й строки делим на 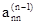 и в результате получаем:
и в результате получаем:

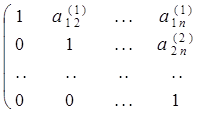
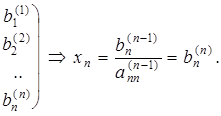
На этом закончился прямой ход метода Гаусса.
5. Выполняем обратный ход метода Гаусса: в (п—1)-ю строку последней матрицы подставляем значение хn и находим значение xn-1, затем последовательно находим xn-2, xn-3, ... , x2, x1 по формулам:
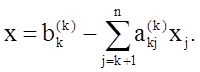
Этот алгоритм является экономичным в смысле использования памяти, так как все промежуточные и окончательные значения элементов в процессе преобразования матриц последовательно хранятся в тех же ячейках памяти, что и массивы А и В. Очередные значения диагональных элементов 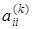 перед началом преобразования строк будем присваивать простой переменной D, что позволит хранить их до окончания преобразования очередной строки матрицы.
перед началом преобразования строк будем присваивать простой переменной D, что позволит хранить их до окончания преобразования очередной строки матрицы.
Значения переменных xn, xn-1, ...,x1 присваиваются элементам массива свободных членов В.
Метод Гаусса с выбором главного элементазаключается в том,что при прямом ходе производится выбор наибольшего по модулю (главного) элемента и перестановка строк или столбцов. Последнее исключает деление на 0, если матрица коэффициентов содержит нулевые элементы, и повышает точность вычислений при наличии ошибок округления. Обычно для программ, ведущих вычисления с числами с плавающей точкой, достаточен выбор Aii ¹ 0.
Метод вращения является разновидностью метода Гаусса. Он обладает повышенной устойчивостью к “провалам” промежуточных вычислений. Этот метод обеспечивает приведение исходной системы к системе с верхней треугольной матрицей (см. литературу).
4.2 Правило Крамера
Правило Крамера рассмотрим на примере двух линейных уравнений с двумя переменными:
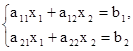 (17)
(17)
хотя оно применимо и для решения системы n линейных уравнений с n переменными, но с увеличением n требует большого объема вычислительной работы.
Умножим первое уравнение системы (17) на коэффициент а22, а второе — на — a12 и полученные уравнения сложим. Тогда имеем:
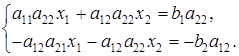
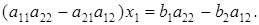
Если a11a22 - a21a12 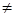 0, то получаем значение переменной
0, то получаем значение переменной
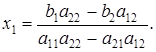
Аналогично, умножая первое уравнение системы (17) на —a21, второе — на а11 и складывая их, получаем:
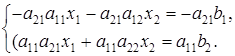
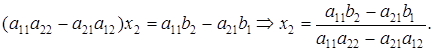
Введем обозначения: a11a22 - a21a12 = 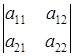 =
=  ;
;
b1a22 - b2a12 = 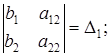
a11b2 - a21b1 = 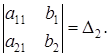
Следовательно,  — определитель матрицы коэффициентов системы (17). Определитель
— определитель матрицы коэффициентов системы (17). Определитель 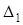 получается из определителя
получается из определителя  , если коэффициенты системы (17) при x1 (первый столбец матрицы А) заменить свободными членами
, если коэффициенты системы (17) при x1 (первый столбец матрицы А) заменить свободными членами
B = 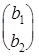 ;
;
Определитель 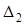 — если заменить коэффициенты системы (17) при x2 (второй столбец матрицы А) свободными членами.
— если заменить коэффициенты системы (17) при x2 (второй столбец матрицы А) свободными членами.
Определитель  называется главным определителем системы (17), а определители
называется главным определителем системы (17), а определители  1 и
1 и  2 — вспомогательными.
2 — вспомогательными.
Если главный определитель 
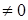 , то матрица
, то матрица 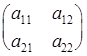 называется неособенной, в противном случае - особенной.
называется неособенной, в противном случае - особенной.
Таким образом, если главный определитель системы уравнений (17) 
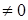 , то система имеет единственное решение, определяемое формулами
, то система имеет единственное решение, определяемое формулами
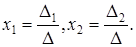 (18)
(18)
Формулы (18) называются формулами Крамера.
Нахождение решения линейной системы (17) по формулам (18) называется правилом Крамера, который одним из первых пришел к понятию определителя и доказал сформулированное выше предложение.
Справедливы также следующие два предложения:
1. Если главный определитель системы (17)  = 0, но хотя бы один из вспомогательных определителей
= 0, но хотя бы один из вспомогательных определителей  1 или
1 или  2 отличен от нуля, то система (17) не имеет решений (система несовместна).
2 отличен от нуля, то система (17) не имеет решений (система несовместна).
2. Если все три определителя  ,
,  1 и
1 и  2 системы (17) равны нулю, но среди коэффициентов аij(i, j = 1,2) есть хотя бы один, отличный от нуля, то система (17) имеет бесконечное множество решений.
2 системы (17) равны нулю, но среди коэффициентов аij(i, j = 1,2) есть хотя бы один, отличный от нуля, то система (17) имеет бесконечное множество решений.
Легко дать геометрическое истолкование этим предложениям. Поскольку каждому уравнению системы (17) в плоскости соответствует некоторая прямая, то система (17) имеет единственное решение, если прямые имеют одну общую точку; не имеет решений, если прямые параллельны; и имеет бесконечное множество решений, если прямые сливаются.
Правило Крамера решения системы n линейных уравнений с n переменными имеет определенное теоретическое значение; практически им уже при n = 4 не пользуются. Установлено, что число операций умножения и деления, которые необходимо выполнить при решении линейной системы алгебраических уравнений порядка n по формулам Крамера, равно:
N(n)= (n2 — 1)n! + n,
а по схеме единственного деления метода Гаусса:
N(n) = 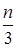 (n2 + 3n — 1).
(n2 + 3n — 1).
Для сравнения объема вычислительной работы по этим двум алгоритмам подсчитаем количество операций:
по Крамеру по Гауссу
при n = 5 2885 65
при n =10 360*106 430
Поэтому все современные ЭВМ имеют стандартные подпрограммы, реализующие различные модификации метода Гаусса.
4.3 Метод итераций и метод Зейделя
Метод итераций позволяет получить последовательность приближенных значений, сходящуюся к точному решению системы линейных уравнений. В отличие от метода Гаусса, метод итераций не требует контроля промежуточных вычислений, так как отдельные ошибки на каком-либо шаге итерации не искажают окончательных результатов, хотя и удлиняет процесс счета. Иначе говоря, метод итераций решения систем линейных уравнений является самоисправляющимся. Кроме того, метод итераций легко запрограммировать для ЭВМ. Пусть имеем систему
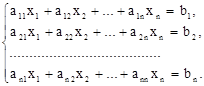
или, короче,
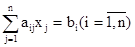 . (19)
. (19)
Предположим, что определитель системы отличен от нуля и что диагональные коэффициенты 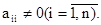
Выразим из первого уравнения x1, из второго x2, и т. д. Тогда получим эквивалентную систему:
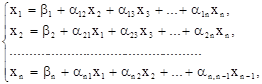
где 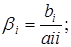

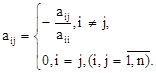
Полученную систему запишем так:
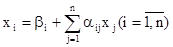 (20)
(20)
и назовем ее системой нормального вида.
Будем решать ее методом последовательных приближений. За нулевое приближение возьмем, например, столбец свободных членов

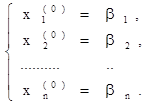
Подставив в правую часть системы (20) значения 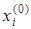 (i =
(i = 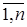 ), получим первое приближение:
), получим первое приближение: 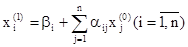 .
.
Затем аналогично второе: 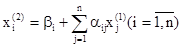 и т. д.
и т. д.
Таким образом, зная k-e приближение, (k + 1)-е приближение вычисляют по формуле 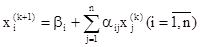 (21)
(21)
Если последовательность приближений ( 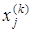 ) (j =
) (j = 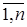 ) имеет предел
) имеет предел
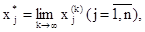
то 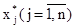 является точным решением системы нормального вида, а значит, и исходной системы. В самом деле, переходя к пределу при
является точным решением системы нормального вида, а значит, и исходной системы. В самом деле, переходя к пределу при 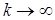 в (21), имеем:
в (21), имеем:
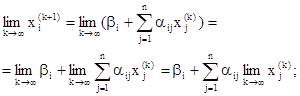
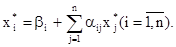
Описанный метод последовательных приближений называется методом итераций. Рабочие формулы метода итераций имеют вид:
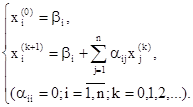 (22)
(22)
Существование предела
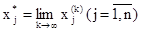
гарантирует теорема о достаточном признаке сходимости процесса итераций.
Достаточным условием сходимости итерационных методов является условие
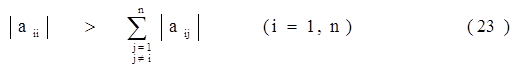
При методе Зейделя итерационный процесс подобен описанному для метода простых итераций, однако уточненные значения Хij+1 сразу подставляются в последующие уравнения. Формула итерационного процесса имеет вид:
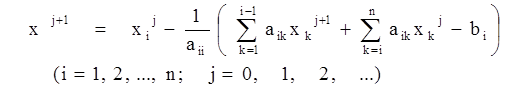
Дата добавления: 2015-03-11; просмотров: 1588;
