Численное дифференцирование

В инженерной практике довольно часто приходится встречаться с обыкновен­ными дифференциальными уравнениями при решении различных прикладных задач. Обыкно­венным дифференциальным уравнением называется выражение вида

F(X,Y,Y',Y”,...,Y ^n-1 ,Y ⁿ ) = 0 , (1)

где Х - независимая переменная;

Y - искомая функция от Х;

Y',Y»,...,Yⁿ -производные порядка 1,2,...,n.

Порядок старшей производной, входящей в уравнение (1), называется порядком дифференциального уравнения.

Простейшим обыкновенным дифференциальным уравнением является уравнение 1-го порядка

y'= f(x,y) (2).

Основная задача, относящаяся к этому уравнению, есть задача Коши: найти реше­ние дифференциального уравнения (2) в виде у=у(х), удовлетворяющее начальному усло­вию Y(Xo)=Yo, т.е. требуется найти интегральную кривую у=у(х), проходящую через заданную точку М(Хо,Yo).

Для нахождения решения дифференциального уравнения (1) необ­ходимо задать та­кое количество начальных условий, какое соответствует порядку старшей производ­ной, а именно задать значения

Yo=Y(Xo); Yo'=Y'(Xo),...,Y₀ ^n-1 = Y^n-1 (Xo) (3)

Уравнение (1) называется разрешенным относительно старшей производной, если оно имеет вид

Y⁽ⁿ⁾ =f(X,Y,Y',Y»,...,Y^n-1 ) (4)

Если дифференциальное уравнение (1) разрешимо относительно старшей произ­водной, то его можно свести к системе обыкновенных дифференциаль­ных уравнений 1-го порядка заменой на неизвестную функцию Р₁(х), у» на Р₂(х) и т.д.

Таким образом, имеем

y'=P₁,

P1'=P₂,

P2'=P₃,

...

P'n-1 = f (x,y,P₁,P₂,...,P_n-1), причем

Y(Xo)=Yo

P₁(Xo)=Yo'

P₂(Xo)=Yo»

. . . . . . . . .

P _n-1(Xo)=Yo^n-1 .

При решении инженерных задач чаще всего приходится иметь дело с уравне­ниями, общее решение которых не выражается в аналитическом виде. Поэтому возникает необходимость применять те или иные методы, дающие приближенное ре­шение задачи.

6.1 Метод Эйлера

Метод численного решения дифференциального уравнения 1-го по­рядка

y'=f(x,y) (7)

с начальным условием Y(Xo)=Yo основан на разложении решения в ряд Тейлора в h-окрестности точки Хо:

Y1 = Y(x+h) = Y(Xo) + h*Y'(Xo) + (h²/2)*Y»(Xo) +...

При отбрасывании всех членов ряда, содержащих производные 2-го и высших порядков, получим

Y1 = Yo + h*f(Xo,Yo),

где f(x,y) - правая часть уравнения (7). Пользуясь значением Y1 из разложения y(x) в h –окрестности точки Х1=Хо+h, получим

Y2=Y1+h*f(X1,Y1),

аналогично продолжая для следующей Х i+1 точки, получим

Y i+1 = Yi+h*f(Xi,Yi). (8)

Если дано уравнение 2-го порядка

Y»=f(x,y,y') (9)

c начальными условиями Y(Xo)=Yo и Y'(Xo)=Yo', то такое уравнение можно свести к системе двух уравнений 1-го порядка

у'=P (10)

P'=f(x,y,y'),

причем

Y(Xo)=Yo, (11)

P(Xo)=Po=Yo'.

Тогда приближенные значения функций у и Р в точке можно вы­числить

Y_i+1 = Y_i+h*P_i (12)

P_i+1 = P_i+h*f(X_i, Y_i, P_i),

где f( Xi, Yi, Pi) - правая часть уравнения (9).

При достаточно малой величине шага h метод Эйлера дает реше­ние с большой

точностью, т.к. погрешность решения близка к h².

Разновидностью рассмотренного выше метода Эйлера, известного в литературе также как метод Эйлера-Коши, является метод Эйлера-Коши с итерациями. Он заключается в вычислении на каждом шаге начального значения

Y⁰_i+1=Y_i+hF(x_i ,Y_i).

Затем с помощью итерационной формулы

Y^к_i+1=Y_i + 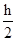+ [ F(x_i, Y_i) + F(x_i+1, ]

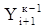решение уточняется. Итерации проводят до тех пор, пока совпадает заданное число цифр результата на двух последних шагах итераций. Погрешность метода составляет примерно h³. Обычно число итераций не должно превышать 3-4, иначе нужно уменьшить шаг h.

Модифицированный метод Эйлера второго порядкареализуется следующими рекуррентными формулами:

Y_i+1 = Y_i + hF(x_i + h/2, Y^*_i+1/2 ),

где Y^*_i+1/2 = Y_i + hF(x_i , Y_i)/2 . Метод дает погрешность порядка h³ и имеет меньшее время вычислений, поскольку вместо нескольких итераций производится вычисление только одного значения Y^*_i+1/2.

Метод трапеций – одна из модификаций метода Эйлера второго порядка. Он реализуется применением на каждом шаге формулы

Y_i+1 = Y_i + 0.5(K₁+K₂)

где K₁ = h F(x_i,Y_i);

K₂ = h F(x_i+h,Y_i+K₁)

и дает погрешность порядка h³. Этот метод относится к общим методам Рунге-Кутта.