ТРЕХМЕРНОЕ ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ АЭРОДИНАМИКИ ТОПОЧНОЙ КАМЕРЫ, ОБОРУДОВАННОЙ СИСТЕМОЙ ТЕРМИЧЕСКОЙ ПОДГОТОВКИ ТОПЛИВА

Как было выше отмечено, повышение эффективности энергетического использования Канско-Ачинских углей может быть достигнуто путем их предварительной термической подготовки в условиях ТЭС.

Прототипом для численного моделирования послужило техническое решение, основанное на использование внутритопочной термической подготовки для котла Е-500 и защищенное патентом на изобретение [268].

Топочная камера котла Е-500 представляет собой призматическую топку глубиной 10,5 м, шириной 11,5 м. В предлагаемом техническом решении участки соединения стен топочной камеры отделяются от камеры горения топки двусветными газоплотными экранами, образуя тем самым камеры термической подготовки равнобедренного треугольника сечения с размерами сторон 3 х 3 х 3 и высотой 10 м.

Конструктивные характеристики камер термической подготовки получены исходя из условия обеспечения температуры в зоне термоподготовки 800Спри длительности пребывания угольных частиц 2,5 ÷ 1,75 с. Высокотемпературные дымовые газы из топки поступают в верхнюю часть камер термической подготовки, где происходит термоокислительный пиролиз угольной пыли. Продукты термоподготовки воспламеняются за счет вторичного воздуха, подаваемого через воздушные шлицы вторичного дутья, тангенциально к условной окружности. Равномерное распределение теплонапряжения топочного объема осуществляется за счет организации ступенчатого сжигания, для чего установлены сопла третичного дутья.

Настоящие исследования проводились как начальный этап выполнения поставленной задачи с целью проверки работоспособности предлагаемого технического решения в целом, а также для получения данных о структуре пылеугольного потока, необходимых при огневом моделировании. Следует отметить, что численное моделирование аэродинамики рециркулирующих турбулентных многофазных потоков является самостоятельной инженерной задачей, вызванной сложной конфигурацией реальных энергетических объектов (криволинейные ограничивающие поверхности, множественность входов, наличие внутренних перегородок, разветвление потоков, отсутствие осей или плоскостей симметрии), обуславливающих необходимость применения неортогональных криволинейных координат, согласованных с границей моделируемого агрегата, как правило, в пространстве трех измерений [291].

Согласно существующим представлениям [292], достаточно реалистичная картина трехмерных реагирующих течений может быть получена на основе совместного решения системы уравнений динамики вязкого газа и движения частиц в потоке. Уравнение неразрывности для газовой среды используется в следующей форме:

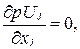(6.1)

где j = 1, 2, 3. Уравнение баланса количества движения по трем осям координат, i = 1, 2, 3, j = 1, 2, 3, имеет следующий вид:

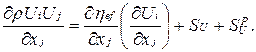(6.2)

Для расчетов турбулентных течений используется стандартная 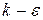модель турбулентности Харлоу [283] турбулентной вязкостью 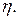Стандартная 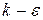модель турбулентности состоит из уравнений баланса турбулентной кинетической энергии 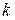и скорости диссипации турбулентной кинетической энергии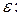

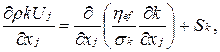(6.3)

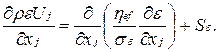(6.4)

Коэффициент эффективной вязкости определяется по следующей зависимости:

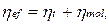(6.5)

где 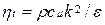– коэффициент турбулентной вязкости; 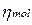– молекулярная вязкость газа (принимается равной вязкости воздуха как функция от температуры).

Уравнение динамики решалось с использованием следующих граничных условий: на входной границе компоненты скорости рассчитывались исходя из заданного массового расхода, плотности входного потока, площади горелочного устройства и угла наклона его к нормали:

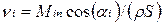. (6.6)

Величина 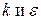оценивались на основе соотношений:

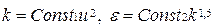. (6.7)

На выходе из топочной камеры ставится условие отсутствия осевых градиентов («мягкие» условия):

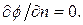(6.8.)

Для уменьшения вычислительных затрат используется известный метод пристеночных функций для решения уравнения количества движения и k-s модели турбулентности вблизи стенок. Согласно методу, отпадает необходимость интегрирования основных уравнений вплоть до физической стенки, так как при этом потребуется значительное количество дополнительных расчетов узлов вблизи ее. Взамен для ближайших к стенке узлов привлекается полуэмпирическая информация. Например, для скорости U задается логарифмический закон изменения. Уравнения (6.1 ÷ 6.7) можно представить в виде одного уравнения:

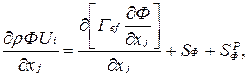(6.9)

где 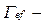коэффициент переноса; 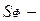источниковые члены, значения которых оцениваются по формулам, представленным в табл. 6.1.

Запись уравнений в общем виде (6.9) позволяет создать единый метод решения для зависимостей различного физического наполнения. Приведенные выше математические выражения записаны в декартовой системе координат, однако топочная камера парового котла с зонами пылеподогрева топлива представляет собой сложный геометрический объект, который можно описать только при использовании криволинейных координат.

При переходе к криволинейной системе координат уравнение (6.9) трансформируется к виду

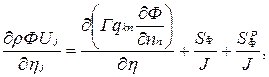(6.10)

где 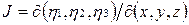– якобиан перехода.

Таблица 6.1

Значения коэффициента перноса и источниковых членов

Ф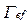
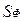
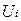
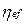
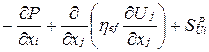
k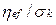

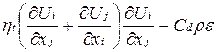
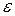
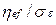
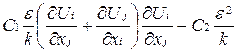
В развернутом виде якобиан перехода представляет собой матрицу следующего вида:

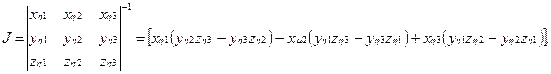
Скорости переноса U, V, W в новой системе координат вычисляются по уравнениям:

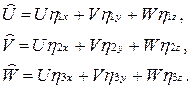
Метрические коэффициенты определяются по следующим соотношениям:

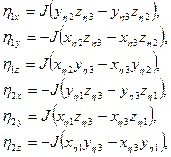
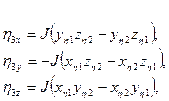
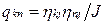– суммирование по повторяющим индексам.

Источниковый член S для всех скоростей U, V, W имеет следующий вид:

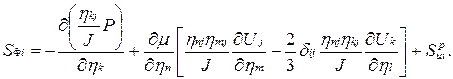(6.11)

Для остальных компонентов источниковые члены записываются с использованием якобиана преобразований аналогично. Представленные дифференциальные уравнения сильно нелинейны и взаимосвязаны. Особый характер имеет взаимная зависимость составляющих скорости, так как каждая из них содержит неизвестный градиент давления, и при этом все составляющие скорости дополнительно связаны уравнением сохранения массы, в котором отсутствует давление. Вследствие невозможности получения аналитиеского решения для получения результатов часто используют численные методы. В данной работе использовалась процедура SIMPLEC [292], предназначена для решения уравнения скорости и давления.

Для описания дисперсной фазы применяется так называемый лагранжев подход моделирования поведение отдельной частицы и специальная методика определения [279, 293-294], заключающаяся в подразделении на ряд классов всей совокупности частиц, поступающих в расчетную область. Из каждого класса выбирается «полномочный» представитель, т.е. отдельная частица, для которой решаются уравнения движения. При этом делаются допущения, что все остальные частицы данного класса ведут себя точно так же. как и представитель. При этом две частицы относятся к одному классу, если они имеют одинаковый размер и если они попадают в топку в одном и том же месте входного окна. В практических расчетах число классов составляет порядка сотен, а число частиц в классах порядка миллиона. Например, если взять пять фракций N = 5 и шестьдесят мест старта М = 60, тот вся совокупность частиц разбивается на 5 х 60 = 300 классов.

При описании движения частиц в потоке использовалось следующее уравнение:

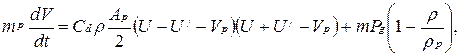(6.12)

где 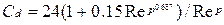– коэффициент сопротивления; 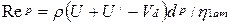– число Рейнолдьдса для частиц.

Вектор 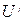учитывает влияние турбулентных флуктуаций скорости газа на движение частиц и находится на основании случайного распределения Гаусса для всех трех направлений в зависимости от известной локальной турбулентной энергии и масштаба турбулентности. Время, в течение которого случайная флуктуация скорости газа воздействует на частицу, определяется как минимум между временем жизни соответствующего турбулентного вихря и временем пересечения частицей этого вихря.

Угольные частицы, переносимые потоком газа, оказывают влияние на количество движения газа. Учет этого эффекта производится через источниковые члены 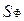, присутствующие в уравнении (2.9). Рассмотрим эти источники более детально. Пусть индекс i обозначает номер функции частиц (i = 1, 2, 3… , 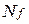, где f - доля данной функции), а индекс j - стартовую координату частицы (j = 1, 2, 3,…, 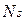, где s - доля частиц, стартующих с места j). Тогда число частиц фракций i, стартовавших с j-го места в единицу времени, выражается формулой:

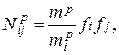(6.13)

где 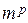– общий массовый расход угля; 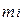– масса частицы угля i-й фракции.

Источник импульса для газового потока в некотором контрольном объеме 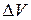от частиц одного класса равен разнице импульса потоков частиц на входе для данного объема:

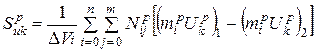. (6.14)

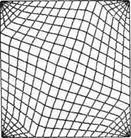
Уравнения (6.7 ÷ 6.14) составляют численную модель трехмерного стационарного течения газа при наличии угольных частиц, основанную на использовании полных осредненных уравнений Навье-Стокса, замыкаемых полуэмпирической 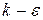моделью. Уравнения решаются в обобщенной криволинейной системе координат. Расчетная сетка топочной камеры котла Е-500-140 применительно к прорабатываемому техническому решению представлена на рис. 6.1 и имеет размер 25 х 25 х 33.

Для построения сетки возникла необходимость использования алгебраических методов. Для детального описания геометрии топки с выделенными отсеками под термическую подготовку топлива применялся блочный метод. Низ пылеподогревателя располагается на отметке 18 м (15-я ячейка), а верх на отметке 26,5 м (21-я ячейка). Сопла воздушного дутья располагаются в два яруса на высотах 13,6 м (8-я ячейка) и 18 м (13-я ячейка). Сопла направлены по касательной к воображаемой окружности с диаметром 1,1 м.

			в)

Рисунок 6.1 – Расчетная сетка топки котла Е-500-140 с внутренним пылеподогревателем: а – общий вид; б – вертикальное сечение; в – горизонтальное сечение

Численные исследования аэродинамики выполнены в два этапа. На первом этапе моделировалась картина течения воздушных струй при измененной конфигурации топочной камеры и профиля горелок вторичного дутья. На втором – осуществлялась проверка работоспособности и надежности аэродинамической схемы предлагаемой системы при наличии угольных частиц различного размера и плотности.

На рис. 6.2 приведены картины течения и взаимодействия струй при расчете структуры скоростей без угольных частиц. Все изображения представлены в масштабе, а длина стрелочки, обозначающей вектор скорости, соответствует величине его модуля. Если показано только окончание вектора, то это означает, что его длина вне пределов разрешимости и поэтому указывается только направление. Из рис. 6.2 г, д видим, что в горизонтальных сечениях образуется устойчивый вихрь, заполняющий топочную камеру и распространяющий до выходного окна (до ширм).

Так как топочная камера в области пылеподогревателей имеет восьмигранную форму, близкую к цилиндрической, то, в отличие от типовой топочной камеры прямоугольной формы, происходит более полное заполнение топочного пространства, характеризующееся отсутствием застойных зон и прямого наброса факела на стены. В вертикальных сечениях (рис. 6.2 а, б, в) наблюдается подъемное движение с прогибом в центре.

Данный прогиб вызван наличием вихря в горизонтальной плоскости. Поджатие потока в области пылеподогревателя и организация крутки потока плоскими воздушными струями приводят к более равномерному профилю аксиальной скорости на выходе из топки по сравнению с течением в топке Е-500-140 без зон с пылеподогревом.

В области холодной воронки можно отметить слабые вихри. По краям холодной воронки заметно опускное течение, а в центре – подъемное. Так как подаваемая струя являются узкими по вертикали, поэтому исследовалась возможность взаимодействия струй между собой и отрицательного влияния друг на друга. С этой целью один блок сопл направлен под углом 10 градусов вверх, а противоположный – направлен под углом 10 градусов вниз, два других блока оставались неизмененными и не имели наклона вверх и вниз. Выявлена устойчивая структура течения, система оказалась жесткой к таким возмущениям.

На рис. 6.2 а, е представлена схема течения в зонах предварительной термической подготовки топлива. Получено равномерное заполнение потоком по сечению при стабильном характере профиля скорости вдоль всей высоты канала.

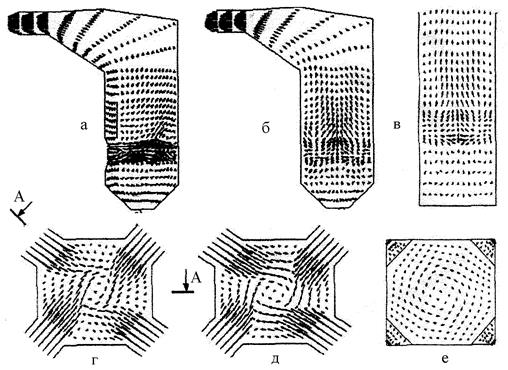
Рисунок 6.2 – Картины течения в различных сечениях топочной камеры: а – вертикальное сечение через пылеподогреватель; б – вертикальное продольное сечение по центру; в – вертикальное поперечное сечение по центру; г – горизонтальное сечение на уровне первого яруса горелок; д – горизонтальное сечение на уровне второго яруса горелок; е – горизонтальное сечение на середине пылеподогревателя

В верхней части отсеков пылеподогревателя наблюдается устойчивая эжекция топочных газов в зону термообработки (рис. 6.2 а). Для эжекции по результатам материального баланса составляет 10 – 15 % от общего расхода продуктов сгорания в верхнюю часть топки.

Средние скорости в пылеподогревателе составляют 7 – 8 м/с. Доля эжекции газов в каждую секцию подготовки топлива одинакова.

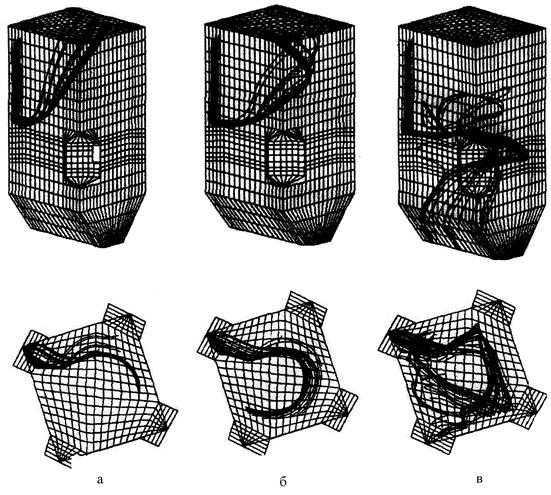
Рисунок 6.3 – Траектории движения угольных частиц различного размера
(р_m = 1200 кг/м³) в топке котла: а – 100 мкм; б – 300 мкм; в – 500 мкм.

Траектории движения пылеугольных частиц в топочной камере представлены на рис. 6.3 и 6.4. Для составления реальной картины поведения частиц в потоке расчет выполняется на различный размер частиц: 30, 100, 300, 500, 800 мкм, а также на различную плотность: 1200 и 2400 кг/м³ .

Угольные частицы с размером менее 500 мкм подчиняются аэродинамической структуре газового вихря, а общий вектор скорости направлен в сторону выходного окна, что вполне согласуется с траекторией таких частиц в существующей схеме сжигания. Частицы с размером 500 мкм и выше выпадают из газового потока и сепарируются, что может вызвать к ужесточению требований к тонине помола.

Рисунок 6.4 – Траектории движения угольных частиц различного размера
(р_m = 2400 кг/м³) в топке котла: а – 100 мкм; б – 300 мкм; в – 500 мкм

При увеличении плотности угольных частиц наблюдается некоторое изменение траектории движения частиц отдельных классов, хотя общая закономерность их поведения по отношению к частицам меньшей плотности остается постоянной.

Выводы

Численный эксперимент показал, что рассмотренная конструкция высокоэкономичного котельного агрегата с внутритопочной термической подготовкой позволяет организовать эффективную аэродинамику топочной камеры и обеспечить более равномерное заполнение объема топочной камеры продуктами горения; ликвидировать образование локальных высоких лучистых тепловых потоков.

Это приведет к уменьшению образования термических оксидов азота и более полному выгоранию потока угольной пыли; равномерной и глубокой термической обработке минеральной части, что дополнительно снизит шлакование экранных труб и уменьшит загрязнение конвективных поверхностей нагрева.