Решение задач интерполяции и экстраполяции
Пусть на интервале [a,b] заданы n+1 опорных (узловых) точек a £ xo< x1 < x2 <...< xn £ b. Пусть, кроме того, заданы n+1 действительных чисел yi(i=0, 1,2,...,n) (например, как значения функции в узловых точках). Под задачей интерполяции понимают нахождение многочлена In(x) степени не больше n такой, что In(xi)=yi для 0 £ i £ n.
Интерполяцию обычно применяют тогда, когда относительно f известны только дискретные значения функции y=f(x), и, чтобы вычислить другие ее значения между узловыми точками (интерполяция) или за отрезком узловых точек (экстраполяция), ее приближают многочленом In(x), причем f(xi)=In(xi) (i=0,1,2,...,n).
Всегда существует только один интерполяционный многочлен, который может быть представлен в различной форме.
Форма Лагранжа: In(x)=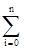 
yi×Li(x);
Li(x)= 
.
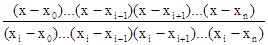Нетрудно видеть, что Li(xi)=1, Li(xk)=0 при k¹j, и, следовательно, Ln(xi)=yi.
Форма Ньютона: In(x)= 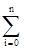сiNi(x), N0=1,
Ni(x)=(x-x0)(x-x1)...(x-xi-1) (i=1,2,...,n),
Ci(i)=[x0x1x2...xi]=[xixi-1xi-2...x0],
где [xixi-1xi-2...x0]=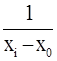 
([xixi-1xi-2...x1]-[xi-1xi-2...x0]),
[xi]=yi (i=0,1,2,...,n).
Выражение [x0x1x2...xi] называется разделенной разностью. Для определения многочлена в форме Ньютона применяют разностную схему или схему спуска (см. литературу).
Пример. Нахождение интерполяционного многочлена.
Пусть после опыта получены следующие пары: x1=4, y1=1; x2=6, y2=1; x3=8, y3=1; x4=10, y4=1.
Многочлен Ньютона I3(x)=
=1+1×(x-4)+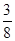 
(x-4)(x-6)+ 
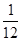(x-4)(x-6)(x-8)= 
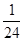(2x3-27x2+142x-240).
Дата добавления: 2015-03-11; просмотров: 1465;