Вычисление суммы функционального ряда
Пусть задан некоторый ряд слагаемых a1(х)+a2(х)+a3(х)+...+an(x) и необходимо найти его сумму. Если слагаемые зависят от некоторого параметра Х и номера n, определяющего место этого слагаемого в ряде, то такой ряд называется функциональным.
Если слагаемые зависят только от номера, то такой ряд называется числовым. Обычно функциональные и числовые ряды задаются в виде формулы общего члена ряда, которые по методам вычисления можно разбить на три типа:
| Тип | Формулы общего члена ряда |
| I | 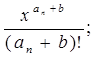 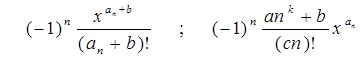
|
| II | 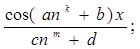 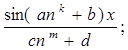 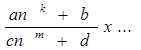
|
| III | 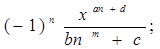 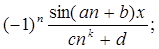 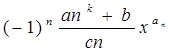
|
где m,n,k - целые числа;
a,b,c,d - действительные числа.
1. Для вычисления члена ряда типа 1 наиболее удобно использовать рекуррентные соотношения, т.е. последующий член ряда находить через предыдущий, что существенно сократит объем вычислительной работы, особенно при вычислении факториалов. Вычисление последующего члена ряда можно представить в виде рекуррентной формулы: А[n+1]=A[n]*G(n,x), где G(n,x)=an+1/an .
При использовании рекуррентных формул необходимо определить начальное значение n, c которого выполняются рекуррентные соотношения, а, следовательно, этим определяются начальные значения (выражения для а и S).
2. Если формула общего члена ряда принадлежит типу II, то целесообразнее и эффективнее вычислять каждый член ряда по общей формуле. В задачах данного типа необходимо обратить внимание на определение начального значения n и начальное значение суммы.
3. Если формула общего члена ряда принадлежит типу III, то целесообразно вычисление текущего члена ряда представить как произведение двух или более сомножителей.
Дата добавления: 2015-03-11; просмотров: 3460;
