Анализ размерностей и нормализация уравнений взаимосвязи физических величин.
Основной метод теории подобия – анализ размерностей физических величин, характеризующих состояние объекта исследования, и параметров, которые определяют это состояние. Под размерностью физической величины понимают выражение связи между ней и физическими величинами, положенными в основу системы единиц. Анализ размерностей позволяет определять вид таких уравнений взаимосвязи физических величин в изучаемых явлениях. Базой анализа размерностей служит требование, согласно которому основные уравнения, выражающие связь между переменными и параметрами объекта, должны быть справедливы при любом выборе единиц измерения входящих в них величин; значения переменных определяются решением данной системы уравнений, значения параметров должны быть заданы для решения этой системы. Из этого требования следует, в общем, что все слагаемые каждого уравнения должны иметь одинаковые размерности и, в частности, что с помощью операции, называемой нормализацией (преобразованием), могут быть приведены к безразмерному виду.
Нормализацию обычно проводят в два этапа. На первом этапе все переменные преобразуются к безразмерному виду путем выбора соответствующих масштабов так, чтобы диапазоны изменения всех безразмерных переменных были одинаковы (например, равны 1). При этом масштабные коэффициенты переменных включают в состав коэффициентов соответствующих членов нормализуемого уравнения. На втором этапе все члены уравнения делят на один из коэффициентов, что дает возможность сделать каждый член уравнения безразмерным. Если уравнение имеет начальные и граничные условия, то и они, соответственно, преобразуются.
Нормализованные уравнения содержат, как правило, величины двух типов:
а) безразмерные зависимые и независимые переменные;
б) безразмерные параметры (иногда называют π-комплексами).
Последние включают характерные размеры (масштабы) объекта, а также физические параметры исходного уравнения и граничных условий. Объекты, описание свойств которых сводится к одинаковым безразмерным уравнениям и граничным условиям, независимо от их физической природы относятся к одному классу. Очевидно, что геометрически подобные или даже физически идентичные системы нельзя относить к одному классу, если граничные условия для них не будут представлены одинаково (например, при различных профилях скоростей потока на входе в идентичные аппараты).
Объекты, относящиеся к одному классу и имеющие одинаковые численные значения π-комплексов в уравнениях и соответствующих граничных условиях, подобны, поскольку поля изменения физических характеристик, определяемые безразмерными переменными, отличаются лишь выбранными масштабными коэффициентов, отношения которых задают коэффициентами подобия. Поэтому π-комплексы называют также критериями или числами подобия, равенство которых для объектов, описываемых идентичными безразмерными уравнениями и граничными условиями, обеспечивает их подобие.
Изменение значений критериев подобия означает переход от одного объекта к другому в пределах объектов данного класса. При таком переходе условия подобия не соблюдаются, только при относительно небольших изменениях критериев или изменениях тех из них, которые слабо влияют на решение уравнений, можно говорить о неполном, или частичном, подобии. Такие случаи чаще всего встречаются на практике при изучении подобия реальных объектов. Например, при изменении геометрических размеров технологической установки затрудняется соблюдение постоянства критериев подобия, включающих объемные и поверхностные характеристики аппаратов, т. к. отношение объема к поверхности изменяется пропорционально их размерам.
Размерные физические параметры, входящие в критерии подобия, для подобных объектов могут иметь сильно различающиеся значения; важно только, чтобы мало отличались друг от друга значения самих критериев. Именно это свойство подобных систем составляет основу метода моделирования и позволяет корректно решать задачи масштабирования, т. е. использовать результаты исследований одного объекта при изучении другого, полностью или частично ему подобного, хотя и существенно отличающегося размерами либо режимами работы. Поэтому соблюдение постоянства критериев подобия – решающее условие успешного переноса исследований на иные объекты.
3.10.3. Анализ решения нормализованных уравнений
Важное следствие процедуры нормализации состоит в том, что число критериев подобия в безразмерных уравнениях и их граничных условиях всегда оказывается меньше числа физических параметров, входящих в исходные соотношения. С одной стороны, это устанавливает необходимое количество критериев подобия различных объектов, принадлежащих к одному классу, с другой – упрощает до некоторой степени решение целого ряда сложных задач.
Решения безразмерных уравнений с соответствующими граничными условиями определяют безразмерные переменные объекта как функции независимых переменных и критериев:
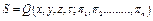 (3.80)
(3.80)
где х, у, z - безразмерные пространств. координаты; τ - безразмерная переменная, соответствующая времени; π1-πn-критерии подобия.
Безразмерный вид функции Q зависит от вида уравнений и граничных условий и обычно не может быть записан в общей форме. Однако сам факт существования зависимости (3.80) приводит к различным выводам. Например, при решении задачи оценки некоторых параметров начальных уравнений по опытным данным выражение (3.80) позволяет установить, какими критериями определяется безразмерный комплекс, включающий неизвестный параметр. Далее можно попытаться найти данную связь в виде некоторой принятой (например, степенной) функциональной зависимости от остальных критериев. Для этого выполняют необходимый объем экспериментов в различных условиях (при которых изменяются значения критериев) и с помощью выбранной зависимости осуществляют соответствующие расчеты наблюдаемых результатов. Полученное соотношение может быть использовано уже для анализа целой группы объектов, критерии подобия которой отвечают изученной области изменения их значений. Такие исследования часто проводят при решении проблем гидромеханики, тепло- и массообмена и т. п. в химико-технологических процессах.
Дата добавления: 2015-01-29; просмотров: 3045;
