Конвективный массообмен
Предположим, что надо определить скорость испарения воды с поверхности озера, когда над его поверхностью дует сухой воздух.
Испарение представляет собой процесс парообразования с поверхности, протекающий при любых температурах и, как правило, одновременно с процессом теплообмена. Поверхность испарения, может уменьшаться (например, при испарении капель), что может оказывать влияние на скорость массообмена.
При испарении жидкости с поверхности необходимо различать испарение со свободной поверхности жидкости (испарение с поверхности водоемов, испарение топлив при хранении и транспортировке и др.) и испарение тонких пленок и капель жидкости (например, топлив) с нагретой поверхности.
При испарении поток паров уносит с поверхности теплоту, необходимую для его образования. В этом случае может иметь место охлаждение поверхности (адиабатическое испарение) и достижение поверхностью некоторой равновесной температуры Тр. Эта температура будет соответствовать равенству тепловых потоков: подводимого к поверхности от окружающей среды с температурой и уносимого с потоком паров.
Так как парциальное давление паров воды в воздухе невелико, то для расчета массового потока с поверхности воды в воздух при температуре Т можно воспользоваться уравнением
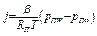 . (3.46)
. (3.46)
Принимая в расчет удельное влагосодержание у испаряющейся поверхности 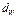 и в окружающем воздухе
и в окружающем воздухе 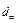 и также используя полученные выражения для
и также используя полученные выражения для 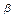 , получим
, получим
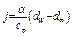 . (3.47)
. (3.47)
Но поскольку массообмен определяется конвективным процессом, то удобно определять поток массы пропорционально разности между массовыми концентрациями на поверхности 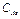 и в окружающей среде
и в окружающей среде 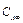 :
:
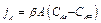 , (3.48)
, (3.48)
где А – площадь поверхности испарения, 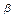 – коэффициент массобмена.
– коэффициент массобмена.
Если принять коэффициенты температуропроводности среды а и диффузии компонента в этой среде D равными, то безразмерные критерии Pr и Sc будут равны и, следовательно равны критерии Нуссельта процессов переноса теплоты и вещества 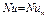 . Значит коэффициент теплообмена равен
. Значит коэффициент теплообмена равен
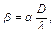 (3.49)
(3.49)
где 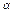 - коэффициент теплоотдачи,
- коэффициент теплоотдачи, 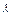 - коэффициент теплопроводности.
- коэффициент теплопроводности.
Если 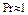 , то
, то
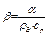 . (3.50)
. (3.50)
Уравнение (3.48) представляет собой все то же выражение (3.39), записанное для удобства аналогично закону Ньютона для конвективной теплопередачи. Соотношение (3.48) поясняет физический смысл коэффициента массоотдачи и математически выражает экспериментально установленный факт, называемый иногда законом Щукарева – количество вещества, перенесенное в единицу времени через единицу площади поверхности, пропорционально разности концентраций у поверхности раздела фаз и в ядре потока.
Также помимо испарения над открытым источником, на практике нередко наблюдается испарение в замкнутый объем. В этом случае плотность массового потока j, удельное влагосодержание d и парциальное давление паров 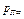 будут меняться в процессе испарения. Дадим приближенный вывод уравнения плотности массового потока паров при испарении воды с поверхности А в ограниченный объем V при постоянной температуре поверхности. Удельное влагосодержание паров в воздухе
будут меняться в процессе испарения. Дадим приближенный вывод уравнения плотности массового потока паров при испарении воды с поверхности А в ограниченный объем V при постоянной температуре поверхности. Удельное влагосодержание паров в воздухе 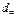 в момент времени
в момент времени 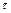 равно
равно
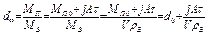 , (3.51)
, (3.51)
где 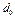 - начальное удельное влагосодержание паров в воздухе.
- начальное удельное влагосодержание паров в воздухе.
Свободный объем есть разность полного объема 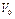 и объема жидкости
и объема жидкости 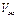 и принимается постоянным,
и принимается постоянным, 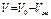 =const. Подставляя значение
=const. Подставляя значение 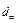 в уравнение
в уравнение
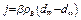 , (3.52)
, (3.52)
Получим
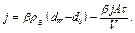 (3.53)
(3.53)
Обозначим 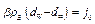 , тогда
, тогда
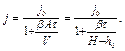 (3.54)
(3.54)
где Н - высота резервуара; 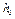 - высота начального столба жидкости (до начала испарения).
- высота начального столба жидкости (до начала испарения).
Если учитывать увеличение свободного объема за счет испарения жидкости
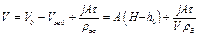 , (3.55)
, (3.55)
где 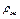 - плотность жидкости, то уравнение массового потока m принимает вид
- плотность жидкости, то уравнение массового потока m принимает вид
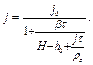 (3.56)
(3.56)
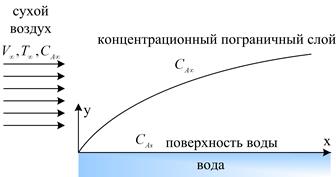
Рис. 3.49. Концентрационный пограничный слой
На рис. 3.49. показана схема физической задачи испарения воды из озера. Эта задача подобна задаче о переносе тепла от: горизонтальной плоской пластины, на поверхности которой развивается тепловой пограничный слой. Аналогичным образом образуется концентрационный пограничный слой, внутри которого концентрация изменяется в направлении, перпендикулярном горизонтальной поверхности озера. Пограничный слой представляет собой область течения вязкой жидкости или газа, образующаяся у поверхности обтекаемого твёрдого тела или на границе раздела двух потоков жидкости с различными скоростями, температурами или химическим составом. Толщина ПС мала по сравнению с продольными размерами. ПС может характеризоваться резким изменением в направлении, поперечном скорости течения различных физических характеристик (скорости течения, температуры, концентрации компонентов). На формирование течения в ПС основное влияние оказывают вязкость, теплопроводность и диффузионная способность жидкости или газа. Тонкий слой, лежащий между твердой границей (стенкой) и внешним потенциальным потоком, обтекающим твердую границу, называется пристеночным пограничным.
Пограничный слой характеризуется тем, что толщина его увеличивается вдоль течения, и движение жидкости в нем не является продольно-однородным.
Течение в пограничном слое слоистое (ламинарное) вблизи точки его зарождения (около передней кромки тела), но постепенно завихряется (становится турбулентным) ниже по течению. Одной из важных проблем является определение положения точки перехода от ламинарного течения к турбулентному. Турбулентный пограничный слой намного толще ламинарного, и их толщины зависят от числа Рейнольдса Re, определяемого как произведение величины на расстояние от передней кромки x. Толщина пограничного слоя δ определяется следующими соотношениями:
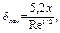 (3.57)
(3.57)
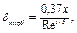 (3.58)
(3.58)
Для определения характера пограничного слоя служит коэффициент Cf. Тело определенной конфигурации имеет свой коэффициент. Так, например, для плоской пластины коэффициент сопротивления ламинарного пограничного слоя равен:
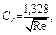 (3.59)
(3.59)
для турбулентного слоя
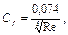 (3.60)
(3.60)
где Re – число Рейнольдса, выражающее отношение инерционных сил к силам трения и определяющее отношение двух составляющих - профильное сопротивление (сопротивление формы) и сопротивление трения.
Снаружи пограничного слоя концентрация водяного пара остается постоянной и равной своему значению в окружающей среде.
Пример задачи об испарении воды из озера далее иллюстрирует подобие между процессами конвективного теплообмена и массообмена. Действительно, если вывести уравнения сохранения для процессов конвективного переноса тепла и массы, то эти уравнения окажутся подобными, причем массовая концентрация Са аналогична температуре Т,а коэффициент диффузии D коэффициенту температуропроводности 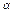 .
.
Эта аналогия предполагает, что простым методом расчета коэффициента массообмена является использование соответствующего безразмерного соотношения для конвективного теплообмена с подстановкой соответствующих безразмерных комплексов, описывающих процесс массообмена. Безразмерным комплексом, описывающим теплообмен, в который входит коэффициент теплоотдачи, является число Нуссельта
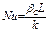 . (3.61)
. (3.61)
Аналогичный безразмерный комплекс, описывающий массообмен, называется числом Шервуда и определяется следующим образом:
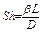 . (3.62)
. (3.62)
В теории теплообмена безразмерным комплексом, который характеризует отношение переноса количества движения к теплопроводности, является число Прандтля
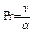 . (3.63)
. (3.63)
В теории массообмена коэффициент диффузии заменяет коэффициент температуропроводности и новый безразмерный комплекс называется числом Шмидта:
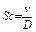 . (3.64)
. (3.64)
Число Шмидта характеризует отношение переноса количества движения к массовой диффузии.
Число Нуссельта является функцией чисел Рейнольдса и Прандтля:
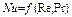
С учетом подобия между процессами конвективного тепло- и массообмена можно ожидать, что число Шервуда будет аналогичной функцией чисел Рейнольдса и Шмидта:
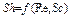
Например, при турбулентном течении в трубе безразмерное соотношение для теплоотдачи (5.12) имеет вид
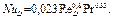 (3.65)
(3.65)
Используя это соотношение, можно приближенно описать поток массы от жидкости, которая полностью смачивает внутреннюю поверхность трубы, к турбулентному потоку газа, протекающему вдоль трубы, с помощью уравнения
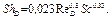 (3.66)
(3.66)
В этом случае жидкость переходит в газовую фазу в результате испарения и уравнение (3.66) можно использовать для расчета скорости испарения жидкости.
В качестве второго примера рассмотрим снова задачу об испарении воды с поверхности озера. Для этого случая конвективный теплообмен описывается соотношением
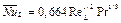 , (3.67)
, (3.67)
которое представляет собой соотношение для расчета теплоотдачи от плоской пластины в предположении ламинарного режима обтекания. Соответствующее соотношение для расчета ламинарного массообмена будет иметь вид
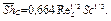 (3.68)
(3.68)
Если в задаче о массообмене перенос осуществляется свободной конвекцией, выражение для коэффициента массообмена можно вывести на основе аналогичной задачи о теплообмене в условиях свободной конвекции. Известно, что теплообмен при свободной конвекции описывается соотношением
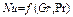
Число Грасгофа для массообмена определяется следующим образом:
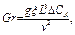 (3.69)
(3.69)
где 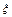 определяется в виде
определяется в виде
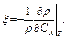 (3.70)
(3.70)
Можно ожидать, что для массообмена при свободной конвекции будет справедливо соотношение в виде
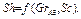
Аналогию Рейнольдса, которая связывает плотность теплового потока и касательное напряжение на поверхности, можно распространить на случай массообмена. Выражение имеет вид
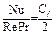 , (3.71)
, (3.71)
Аналогия Рейнольдса для турбулентного массообмена записывается так:
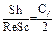 , (3.72)
, (3.72)
В целом процесс стационарного испарения капли характеризуют две величины коэффициент испарения 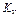 и временем испарения капли
и временем испарения капли 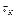 .
.
Скорость испарения капли прямо пропорциональна радиусу капли, коэффициенту диффузии паров и перепаду концентраций.
Так как в процессе испарения капли происходит уменьшение ее радиуса, скорость испарения является переменной величиной (уменьшается в процессе испарения). Поэтому при строгом подходе испарение капли надо рассматривать как нестационарное. Поэтому для произвольного момента времени с помощью текущего радиуса капли R можно найти скорость испарения капли:
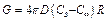 . (3.73)
. (3.73)
Однако скорость испарения капли представляет собой скорость убывания ее массы во времени
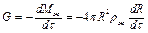 , (3.74)
, (3.74)
Приравнивая два последних уравнения и интегрируя при условии, что испарение капли происходит при постоянной температуре поверхности, получим
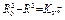 , (3.75)
, (3.75)
где 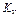 - константа испарения, которая не изменяется в процессе испарения (после ряда допущений),
- константа испарения, которая не изменяется в процессе испарения (после ряда допущений), 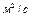 ;
; 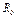 - начальный радиус капли (поверхности).
- начальный радиус капли (поверхности).
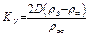 . (3.76)
. (3.76)
Время испарения капли находится при R=0
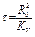 . (3.77)
. (3.77)
При температуре равновесного испарения константа испарения найдется как:
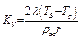 , (3.78)
, (3.78)
где 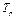 - равновесная температура,
- равновесная температура, 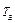 - температура воздуха.
- температура воздуха.
Также говоря о испарении, нужно отметить относительную влажность 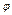 , %:
, %:
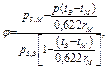 (3.79)
(3.79)
где 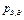 - давление насыщенных паров при температуре воздуха
- давление насыщенных паров при температуре воздуха 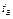 ;
; 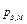 - давление насыщенных паров при температуре поверхности
- давление насыщенных паров при температуре поверхности 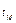 ;
; 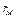 - скрытая теплота парообразования воды при температуре
- скрытая теплота парообразования воды при температуре 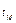 .
.
Пример. Рассчитать скорость испарения воды с поверхности озера имеющего размеры приблизительно 500 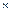 500 м. Скорость ветра 5 м/с. Температура воздуха и воды в озере равна 25
500 м. Скорость ветра 5 м/с. Температура воздуха и воды в озере равна 25 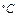 . Давление насыщения водяного пара при 25°С равно
. Давление насыщения водяного пара при 25°С равно 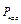 =3098 Н/м2. Коэффициент диффузии равен
=3098 Н/м2. Коэффициент диффузии равен 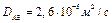 .Рассчитать скорость испарения воды для случаев, когда окружающий воздух имеет относительную влажность а) 10%.
.Рассчитать скорость испарения воды для случаев, когда окружающий воздух имеет относительную влажность а) 10%.
Решение.
Эта задача определяется процессом массообмена при вынужденной конвекции от плоской пластины, Прежде чем подобрать соответствующее безразмерное соотношение для числа Шервуда, следует определить, будет ли течение ламинарным или турбулентным. Число Рейнольдса в конце озера равно
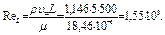
Следовательно, течение воздуха полностью турбулентное и, таким образом, соотношение имеет вид
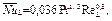
которое используется для расчета турбулентного теплообмена на плоской пластине, Следовательно, соответствующее соотношение для расчета массообмена имеет вид
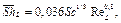
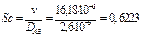
Число Шервуда равно
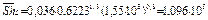
Коэффициент конвективного массообмена равен
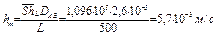
Далее необходимо определить концентрацию паров воды у поверхности озера и в окружающем воздухе, У поверхности воды воздух насыщенный и его относительная влажность равна 100%. Соотношение между парциальным давлением водяного пара, относительной влажностью и температурой насыщения имеет вид
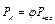
Парциальное давление пара у поверхности озера равно 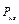 =
= 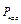 = 3098 Н/м2. Концентрация водяного пара у поверхности озера в предложении, что водяной пар представляет собой идеальный газ, равна
= 3098 Н/м2. Концентрация водяного пара у поверхности озера в предложении, что водяной пар представляет собой идеальный газ, равна
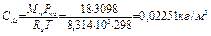
При относительной влажности окружающего воздуха 10% концентрация водяного пара в воздухе равна
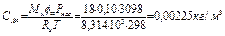
Скорость испарения воды равна
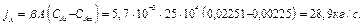
Дата добавления: 2015-01-29; просмотров: 3745;
