Движущая сила массообменного процесса при нелинейной равновесной зависимости. Число единиц переноса и его физический смысл.
Как было указано ранее, движущая сила массообменных процессов определяется степенью отклонения от равновесия. Определяется разностью между рабочей и равновесной концентрациями или равновесной и рабочей, в зависимости от того, какие из них больше. При этом очевидно, что движущую силу можно выражать либо через концентрации распределяемого вещества в фазе G, т. е. через Δy, либо через концентрации его в фазе L, т. е. через Δx.
Ниже указаны возможные варианты выражения движущей силы массообменных процессов при различных направлениях перехода распределяемого вещества. Поскольку концентрации распределяемого вещества можно выражать любыми способами, важно подчеркнуть, что во всех случаях движущей силой процесса будет разность между рабочей и равновесной концентрациями, взятая с положительным знаком.
GèL LèG
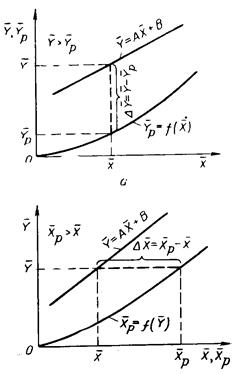
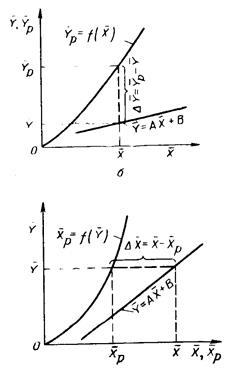
Из изложенного следует, что основное уранвение массопередачи можно записать:
dM=Ky*Δy*F=Kx*Δx*F, то есть Ky*Δy=Kx*Δx
Для одного и того же процесса, как правило Ky≠Kx и Δy≠Δx
Как видно из рисунков, движущая сила меняется с изменением рабочих концентрации, поэтому для всего процесса массообмена, протекающего в пределах концентраций от начальных до конечных, должна быть определена средняя движущая сила (Δyср и Δxср)
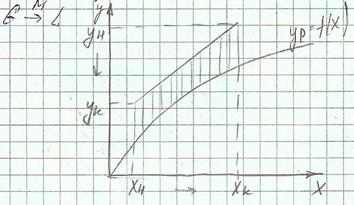 При определении средней движущей силы могут встретиться 2 случая:
При определении средней движущей силы могут встретиться 2 случая:
- зависимость между равновесными концентрациями не линейна; для этого случая равновесная концентрация определяется общей функциональной зависимостью yp=f(x)
- зависимость между равновесными концентрациями линейна, т.е. yp=Ap*x(где Ар – постоянная величина)
Первый случай:
М=G*(yн-yк)=L*(xк-xн)=Ky*Δy*F=Kx*Δx*F
F=G*(yн-yк)/Ky*Δy, где (yн-yк)/Δy=my, аналогично для mx
F=L*(xк-xн)/Kx*Δx, где (xк-xн)/Δx=mx
mx и my – число единиц переноса, которое показывает на сколько единиц изменяется рабочая концентрация под действием единицы движущей силы
Δyср=yн-yк/ 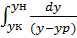
Δxср=xк-xн/ 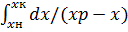
Дата добавления: 2015-01-24; просмотров: 2280;
