Массобмен в системах без твердой фазы . Молекулярная и конвективная диффузия.

В процессах переноса распределяемого вещества (массы) из одной фазы в другую надлежит различать два случая: 1) перенос из потока жидкости в поток жидкости, или массообмен между потоками жидкости, и 2) перенос из твердого тола в поток жидкости (или перенос в обратном направлении), т. е. массообмен между твердой фазой, содержащей внутри пор или капилляров распределяемое вещество, и потоком жидкости.Элементарными законами, которым подчиняется перенос распределяемого вещества из одной фазы в другую, являются закон молекулярной диффузии, закон массоотдачи и закон массопроводности.

Закон молекулярной диффузии или 1ый закон Фика.

Молекулярная диффузия в газах или р-ах жид-ти происходит в результате хаотического движения молекул. Перенос ве-ва осуществляется из области с более высокой концентрации в обл-ть с более низкой концентрацией, независимо от движения потоков.

В этом случае кинетика пр-са подчин. 1му закону Фика: кол-во продифундировавшего ве-ва пропорционально пл-ди перпендикулярной напряж. Диффузионного потока и временем,т.е.

dM=-D* 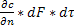(dM-кол-во продифунд.ве-ва;D-коэф.диффузии,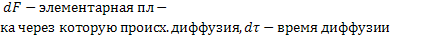

D-показывает какое кол-во ве-ва дифундирует через пов-ть в 1м²в течении 1сек. При разности концентраций на расстоянии 1м=1

Размерность D зависит от 1,от агрегатного состояния сис-мы,2. С увелеичением температ.коэф. диффузии увеличивается.3 с увелич.давления коэф.дифуз.уменьшается.

2.Ковективная диффузия.

В основу рассмотрения явления конвективной диффузии положена теория диффузионного граничного слоя, которую разделяют большинство ученых Советского Союза.

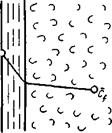
Рис. 11-10. К формулировке закона конвективной диффузии.

Согласно этой теории (рис. 11-10), распределяемое вещество переносится из ядра потока жидкости к границе раздела фаз непосредственно потоками жидкости и молекулярной диффузией. При этом воспринимаю- Г_г(щая распределяемое вещество фаза считается либо твердой, либо близкой к ней (по способности гасить турбулентные пульсации потока). В рассматриваемой системе поток можно считать состоящим из двух частей: ядра и граничного диффузионного слоя. В ядре перенос вещества осуществляется преимущественно токами жидкости и в условиях достаточной турбулентности течения; концентрация распределяемого вещества в данном сечении и в условиях стационарного режима сохраняется постоянной. По мере приближения к граничному диффузионному слою турбулентность и, следовательно, турбулентный перенос затухают, с приближением к границе начинает превалировать перенос за счет молекулярной диффузии. Соответственно этому появляется градиент концентрации распределяемого вещества, растущий по мере приближения к границе. Таким образом, область граничного диффузионного слоя — это область появления и роста градиента концентрации, область увеличения молекулярной диффузии от пренебрежимо малого значения до максимального.

Если рассмотреть элементарный объем фазы (рис. 11-9), перемещающийся в граничном диффузионном слое, то станет очевидной возможность утверждать, что концентрация распределяемого вещества в нем меняется не только за счет молекулярной диффузии, но также и за счет механического переноса его из одной зоны концентрации в другую. В этом случае концентрация распределяемого вещества будет функцией не только пространственных координат и времени, как в случае только молекулярной диффузии, но и компонентов скорости перемещения элемента.

Соответственно этому изменение анализируемого параметра — концентрации С надлежит выразить через субстанциональную производную

DcC/𝜕𝜏=𝜕c/𝜕𝜏+𝜕C𝜕x*wx+𝜕C/𝜕y*wy+𝜕C/𝜕z*wz

При использовании субстанциональной производной приращение количеств распределяемого вещества в элементе за время 𝜕𝜏 может быть выражено как

dM= DcC/𝜕𝜏*dx*dy*dz

Приращение количества распределяемого вещества за счет молекулярной диффузии определяется равенством (11.44). Приравнивая правые части равенств (11.44) и (11.50), получим уравнение конвективной диффузии:

𝜕C/𝜕𝜏+𝜕C/𝜕x*wx+𝜕C/𝜕y*wy+𝜕C/𝜕z*wz=D(𝜕 ²C/𝜕x ²⁺ 𝜕 ²C/𝜕y ²⁺ +𝜕²C/𝜕xz²)

7.Дифференциальные уравнения молекулярной и конвективной диффузии.

Дифференциальное уравнение молекулярной диффузии (второй закон Фика)

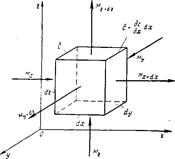
Для вы пода дифференциального уравнения молекулярной диффузии выделим в неподвижной среде или в движущемся ламинарном потоке элементарный параллелепипед с ребрами dх, dу и dz (рис. 11-9).

Если через этот элементарный параллелепипед за счет молекулярной диффузии перемещается распределяемое вещество, то через левую, заднюю и нижнюю грани за время d𝜏 в него входят количества вещества соответственно М_х, М_у и М_z, а через противоположные грани — правую, переднюю и верхнюю — выходят количества вещества соответственно М_х+_d_х, М_у+_d_у и М_г+_dz. Следовательно, элемент за время d𝜏 приобретает диффундирующее вещество в количестве

dM = (М_х - М_х+_d_х) + (М_У- М_у+_d_у) + {М_г – M_z₊_dz)

При этом концентрация диффундирующего вещества повышается на 𝜕С/𝜕𝜏*d𝜏

Согласно основному закону молекулярной диффузии

М_x=-D*𝜕C/𝜕x*dy*dz*d𝜏

Рис. 11-9. К выводу дифференциального уравнения молекул. диффуз

И M_x₊_dx=-D* 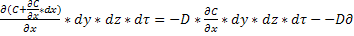²C/𝜕x²*dx*dy*dz*d𝜏

И,следовательно М_x-M_x₊_dx=D*𝜕²C/ 𝜕x²*dx*dy*dz*d𝜏

Аналогично найдем

М_у — М_у+_d_у= D*𝜕²C/ 𝜕x²*dx*dy*dz*d𝜏

М_z— М_z₊_dz= D*𝜕²C/ 𝜕x²*dx*dy*dz*d𝜏

Складывая левые и правые части трех последних равенств, получим

dM=D(𝜕²C/𝜕x²+𝜕²C/dy²+𝜕²C/ 𝜕z²)*dx*dy*dz* d𝜏

С другой стороны, ту же прибыль количества диффундирующего вещества в элементе можно найти умножением объема элемента на изменение концентрации за время d𝜏, т. е.

dM=dx*dy*dz*𝜕C/𝜕𝜏*d𝜏

Сопоставляя соотношения (11.44) и (11.45), получим дифференциальное уравнение молекулярной диффузии:

𝜕C/𝜕𝜏=D(𝜕²C/𝜕x²+𝜕²C/dy²+𝜕²C/ 𝜕z²)

2.Ковективная диффузия.

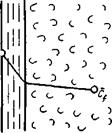
Рис. 11-10. К формулировке закона конвективной диффузии.

DcC/𝜕𝜏=𝜕c/𝜕𝜏+𝜕C𝜕x*wx+𝜕C/𝜕y*wy+𝜕C/𝜕z*wz

dM= DcC/𝜕𝜏*dx*dy*dz

𝜕C/𝜕𝜏+𝜕C/𝜕x*wx+𝜕C/𝜕y*wy+𝜕C/𝜕z*wz=D(𝜕 ²C/𝜕x ²⁺ 𝜕 ²C/𝜕y ²⁺ +𝜕²C/𝜕xz²)

<2 3 456 7 8 >

Дата добавления: 2015-01-24; просмотров: 1951;