Архимед — Лагранж — молекулярная динамика

Две тысячи лет назад Архимед гордо пошутил: «Дайте мне точку опоры, и я переверну земной шар». Двести лет назад Лагранж перефразировал эту шутку: «Дайте мне координаты и скорости всех частиц Вселенной, и я расскажу вам ее прошлое и предскажу будущее». Что имел в виду великий математик и физик?

Ясно, что футбольный вратарь и без Лагранжа может довольно точно предсказать траекторию мяча и своего тела при прыжке — иначе футбольные матчи заканчивались бы со счетом типа 114: 97. Но как объяснить действия вратаря компьютеру?

Второй закон Ньютона F=m∙a (сила F вызывает у массы m ускорение a) относительно легко интегрируется при известной силе F, а значит и ускорении F/m). Если известна скорость V в момент времени t, то через малое время ∆t скорость станет равной V+a∙∆t. Точно так же и координата X через малое время ∆t станет равной X+V∙∆t. Конечно, в пространстве надо рассматривать по три компоненты силы, ускорения, скорости и координаты, но сами формулы (это формулы численного интегрирования уравнений движения) ничуть не станут сложнее. Можно их улучшить, учитывая различными способами тот факт, что даже за малое время ∆t ускорение и скорость могут измениться: это методы интегрирования второго или третьего порядка. Если частиц много, то этот процесс придется повторять для каждой из них.

Вот пример формул численного интегрирования второго/третьего порядка (формулы или алгоритм Верле, 1967г.), использующегося уже в «боевых условиях» настоящих вычислений по методу молекулярной динамики:

Как и раньше здесь выписаны формулы только для одной их трех составляющих. В первой формуле считается, что за время ∆t движение частицы остается равноускоренным; во второй формуле учтено, что сила F зависит от положения частицы, а в третьей – что в качестве ускорения мы берем среднее из ускорений в начале и в конце промежутка ∆t. Отметим, что у уравнений движения есть одна особенность, сильно упрощающая их интегрирование: а именно скорость (первая производная координаты) не зависит явно от самой координаты. Можно считать это подарком физикам от природы.

Перейдем теперь от абстрактных частиц к атомам. Как найти силу F (а значит и ускорение a=F/m), действующую на каждый из многочисленных атомов тела? Удобнее вместо силы рассматривать потенциал — энергию атома U. Тогда компоненту силы легко найти как производную U по соответствующей координате F_x = —dU/dX. Воспользуемся простым приближением парного центрального потенциала. Термин «парный» означает, что U просто складывается из энергий взаимодействия данного атома со всеми остальными, то есть из энергий пар. Термин «центральный» говорит о том, что сила взаимодействия пары атомов направлена по линии, соединяющей их центры, и зависит от расстояния между ними r.

Кое-что о потенциале межатомного взаимодействия можно сказать особого труда. Во-первых, он имеет хотя бы один минимум (но может быть и два, и более) при расстоянии r₀ — это межатомное расстояние в твердом теле при нулевой абсолютной температуре. Если расстояние между атомами больше r₀, то они притягиваются, но максимальная сила притяжения не очень велика — мы можем без труда разорвать проволоку, и представить себе как рвется трос.

Если же расстояние меньше r₀, то действуют силы отталкивания и представить себе два атома на нулевом расстоянии друг от друга — это представить себе термоядерную реакцию между тяжелыми ядрами, те есть процесс, идущий даже не на Солнце, а лишь при взрыве сверхновых звезд (рис. 1).

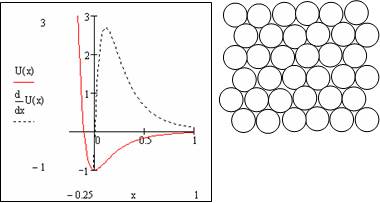
Рис. 1. Потенциал межатомного взаимо­дей­ствия U (красная кривая) и сила взаимодействия (синий пунктир). По оси абсцисс отложена величина ∆r — смещение атома из положения равно­весия. Справа — группа атомов, самопро­­извольно образовавшая при низкой темпе­ратуре кристал­лический кластер. Можно заметить, что из-за тепловых колебаний атомы несколько смещены из узлов решетки.

Как видно из рис. 1 потенциал принципиально нелинеен (точнее нелинейна зависимость F(r)); такие потенциалы называются ангармоничными. Линейность F(r) наблюдается только вблизи нулевой точки. Если бы потенциал был линеен всюду, то колебания атомов были гармоничными (синусоидальными); тепловое расширение отсутствовало бы; твердое тело обладало бы бесконечно большой прочностью; более того, оно никогда бы не плавилось и всегда вело бы себя абсолютно упруго. Таким образом ангармонизм — причина всех этих явлений.

Далеко не всегда достаточно использовать парный центральный потенциал. Ведь в углероде, кремнии и других ковалентных кристаллах атомы удерживаются парой электронов, так что необходимо учесть, что энергия пары атомов зависит от положения хотя бы еще одного, третьего атома («трехчастичный» потенциал); в металлах напротив, ионы удерживаются в положении равновесия коллективизированными электронами и т.д. В идеале нужно использовать расчеты потенциала, основанные на первых принципах («первопринципный» потенциал), но это сама по себе сложная теоретическая и трудоемкая вычислительная задача.

Если мы умеем вычислить потенциал, то уже можно строить модель, позволяющую в результате интегрирования уравнений движения каждого из атомов наблюдать их тепловые колебания, различные перестройки атомной структуры, плавление, кристаллизацию и многое другое. Именно поэтому метод молекулярной динамики стал одним из основных теоретических методов нанотехнологии. В частности его (наполовину всерьез) называют иногда «атомным микроскопом».