Научная рулетка
Какой физический смысл в поговорке «Народу так много – яблоку некуда упасть»? А в ее шуточном антониме «Народу так много – яблоку не на кого упасть»? Каков процент заполнения зала в обоих случаях? Ответ ясен: 100% в первом случае, и 0% во втором. Вот вы и познакомились и даже применили один из самых могучих и широко применяемых в современной физике вычислительных методов — метод Монте-Карло, хотя и в его простейшем варианте. Он разработан в деталях, обоснован, и широко стал применяться в последние 50 лет, но на интуитивном уровне, как вы видели, был известен и раньше. Задачи, решаемые методом настолько разные, что все чаще говорят не о методе, а о методах Монте-Карло.
Рассмотрим теперь один из конкретных и важных примеров. Пусть дана решетка, в узлах которой расположены магнитные моменты известной величины m, которые для краткости будем называть спинами[2]. Между магнитными моментами существует специфическое квантово-механическое взаимодействие электростатического происхождения, называемое обменным взаимодействием[3]. Энергия каждой пары спинов Eij связана с энергией обменного взаимодействия A и взаимной ориентацией двух спинов простым соотношением:
Eij = —A∙cosφij,
где φij — угол между спинами с номерами i и j. Отсюда сразу видно, что если A>0, то энергия минимальна, если φij=0, то есть если спины параллельны. Обменное взаимодействие обладает важной особенностью — фактически оно действует только между соседними спинами и не далее. На первый взгляд кажется, что вся система будет намагничена в одном направлении, но это справедливо лишь если температура равна абсолютному нулю, в противном случае тепловое воздействие будет вызывать хаос и тем больший, чем выше температура — рис.6.
Оказывается с помощью одного из методов Монте-Карло, метода (алгоритма) Метрополиса[4], это нетрудно учесть.
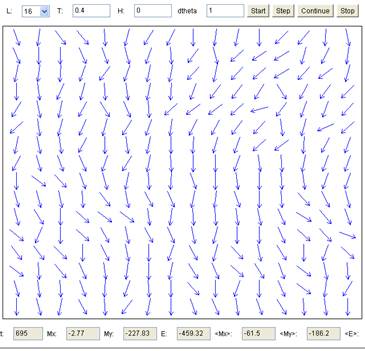
|
| Рис. 6. Магнитные моменты в кристаллической решетке при ненулевой температуре, составляющей 0,4∙A. Видно и премущественное направление магнитных моментов и отклонения от него. |
Для этого рассмотрим изменение энергии пары спинов с номерами i и j (∆Eij) при виртуальном повороте одного из них на некоторый угол. Если эта энергия уменьшается (∆Eij<0), то будем считать, что новая конфигурация будет реализована. Но если энергия увеличивается (∆Eij>0), то новая конфигурация будет реализована с вероятностью W
W = exp(—∆Eij/T),
где Т – абсолютная температура, измеренная в энергетических единицах. Это выражение означает, что из-за действия температуры рост E все же возможен. Реализовать процесс с вероятностью W нетрудно: достаточно выбрать с помощью рандомизатора (процедуры, встроенной в любой язык программирования) случайное число r, с равной вероятностью расположенное между 0 и 1, и сравнить его с W. Если r<W, то виртуальная конфигурация считается реализованной. Выбор числа r эквивалентен случайному бросанию яблока в шуточном примере, с которого мы начали, а сам случайный выбор числа r и дал название метода в честь столицы рулеточного бизнеса.
Можно доказать, что алгоритм Метрополиса реализует вычисление N-мерного интеграла (N – число пар спинов) за счет случайного выбора точек. Очень тщательно исследованы и эффективно применены методы Монте-Карло в работах Вильсона и Кройца по хромодинамике (сильному взаимодействию и кварковой структуре), удостоенных Нобелевской премии за 1983г.
Увеличивая температуру системы можно обнаружить, что при определенной температуре (температуре Кюри) состояние системы изменяется крайне быстро, она переходит из упорядоченного состояния в неупорядоченное, а конкретно из ферромагнитного состояния в парамагнитное. Такое изменение состояния называется фазовым переходом второго рода. Фазовые переходы второго рода играют огромную роль в физике и в технике, на их использовании основан целый ряд устройств, в частности жесткие магнитные диски компьютеров («винчестеры»). Да и вся наша Вселенная возникла в результате фазового перехода второго рода, происшедшего вскоре после Большого Взрыва.
Дата добавления: 2015-02-07; просмотров: 1177;
