Перколяция значит протекание

В середине 50-х годов XX века английский инженер С.Бродбент, изучавший, способы повышения качества угольных фильтров в противогазовых масках шахтеров, столкнулся с проблемой растекания в порах фильтра адсорбированного газа, что совсем не похоже на диффузию. Он увидел, что задача имеет интересную математическую формулировку, и смог заинтересовать задачей математика Д.Хаммерсли. В 1957 году появилась их пионерская работа, в которой описывалась задача, ее некоторые решения и предложен термин перколяция (percolation – протекание). Как всегда бывает с пионерскими работами, она вскоре вызвала лавину (сейчас уже десятки тысяч публикаций) новых формулировок, дополнений, расширений, новых применений и т.д. Теория перколяции позволила впервые после работ Л.Ландау продвинуть теорию фазовых переходов второго рода, она использована как в космологических задачах (образование спиральной структуры галактик); так и в физике полупроводников (электронная примесная проводимость) и т.д.

Еще через десять лет математик Б.Мандельброт ввел понятие фрактала и фрактальной размерности в статье с совсем не математическим названием: «Какая длина у береговой линии Британии?» в авторитетном научном журнале «Science». Эта работа также вызвала огромный интерес, а вскоре выяснилось, что перколяция часто приводит к образованию фракталов. Фрактальные объекты стали ныне настолько популярны, что известны даже и некоторой части широкой публики. Отметим, например, что компьютерные «горные пейзажи» или «плывущие облака» синтезируются именно по фрактальным алгоритмам.

Вот один из скрин-шотов, иллюстрирующий явление ячеечной перколяции и фрактальный объект.

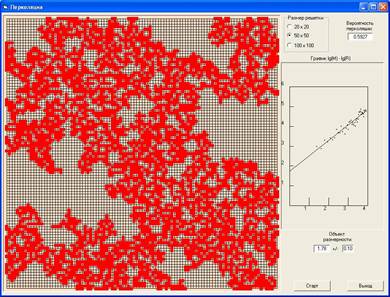
Рис. 7. Одиночный кластер, выросший по перко­ляционному алгоритму из единственной центральной ячейки. Ячейки запол­няются путем «протее­кания» из соседней с ней ячейки с вероятности перколяции p, равной в данном случае 0,5927. На графике справа показана зависимость массы рас­тущего кластера М от его размера R в логариф­мичес­ких координатах.

Второй пример, на рис.8, иллюстрирует одновременное заполнение ячеек с вероятностью перколяции p, причем все соседние заполненные ячейки (кластеры) закрашены одним цветом.

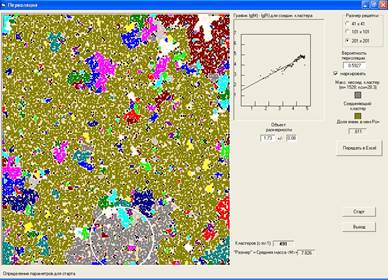
Рис. 8. Ячеечная перколяция в квадратной решетке. Каждая ячейка занимается с вероятностью p. Соседние занятые ячейки образуют кластер. Клас­теры для наглядности раскрашены в разные (случайные) цвета. Соеди­няющий кластер распро­страняется от верхнего края поля до нижнего (или от левого до правого). Окружностью обозначен размер наибольшего несоеди­няющего кластера.

Оказалось, что поведение системы неожиданным образом зависит от значения р, а именно существует критическое значение p_кр (для моделей на рис. 7 и 8 это 0,5927), при котором поведение системы резко меняется. При p<p_кр кластеры как правило быстро останавливаются в росте, поле остается почти пустым; а при p>p_кр кластеры растут неограниченно. Такое поведение системы, которая совсем не похожа на модель Изинга, удивительно напоминает уже описанный выше фазовый переход второго рода, что позволило лучше понять физику фазовых переходов.

Вот некоторые простейшие вопросы, которые возникают при анализе картины перколяции.

Какова вероятность того, что кластер будет неограниченно расти? Как эта вероятность зависит от p? Как менятся средний размер кластера в зависимости от p? Какую роль играет симметрия соседства? А какую роль играет размер решетки? А какую роль играет размерность пространства?

Перколяция оказалось тесно связанной с фракталами. Посмотрим, как это происходит.

Справа на рисунках показана зависимость массы кластера M (на рис. 7 это просто число красных узлов) от его размера R в процессе роста (в логарифмических координатах). Очевидно, что для трехмерных (объемных) объектов:

M~R³;

для двумерных (плоских):

M~R²;

для одномерных (линейных) объектов:

M~R¹.

Вообще для объектов размерности d справедливо, что

M=k∙R^d.

Следовательно, в логарифмических координатах logM=logk+d∙logR и зависимость logM от logR описывается прямой линией, а ее наклон должен равняться d. Но для кластера, показанного на рис. 7, наклон прямой d, найденный методом наименьших квадратов, соответствует ~1.8, а на рис. 8 наклон d равен ~1.7. Это значит, что наши кластеры, расположенные в двумерном пространстве на рис. 7 и 8, – объекты не совсем плоские (d<2)! Но и не линейные (d>1). И береговая линия Британии — вовсе не линия, но и не полоса, а типичный объект с 1<d<2, на что и обратил внимание Мандельброт.

Такие, разреженные, объекты, обладающие дробной размерностью d, получили название фракталов.

С тем, чтобы не отрывать теорию от практики, приведем некоторые, причем далеко не все, примеры прямого применения теории перколяции.

1. Нефтяное месторождение – пористая порода, пропитанная (сверху вниз) слоями газа, нефти и воды в результате миллионов лет «отстаивания» и сепарации. При выкачивании нефти она заменяется водой, которая протекает по капиллярам породы. Неграмотная эксплуатации месторождения может привести к возвращению месторождения в первобытное состояние водонефтяной эмульсии, то есть загубить его на несколько тысяч или миллионов лет вперед.

2. В полупроводниках могут существовать атомы с металлической проводимостью. Если таких атомов много, то они могут образовать бесконечно большой кластер с металлической проводимостью. Макроскопическая модель выглядит так. В ящик поместим смесь пластиковых и металлических шариков. Какова должна быть доля металлических шариков в смеси, чтобы весь ящик был электропроводным?

3. Атомы железа, расположенные в решетке по соседству друг с другом, вступают в обменное взаимодействие и их магнитные моменты упорядочиваются. Сколько в решетке немагнитного вещества должно быть растворено атомов железа, чтобы тело оказалось намагниченным?

4. Как распространяется эпидемия? Как распространяются слухи? Как распространяется лесной пожар?

Темы рефератов и рекомендации по их составлению

1. Области применения метода молекулярной динамики.

Рассмотреть круг задач, которые удается решать методом молекулярной динамики, обратив особое внимание на границы применения метода, то есть на условия, при которых метод не применим.

2. Самоорганизация в больших атомных системах: кристаллические решетки и ее дефекты.

Рассмотреть типы дефектов кристаллической решетки и их роль в формировании свойств кристаллов.

3. Теории потенциала межатомного взаимодействия.

Рассмотреть наиболее распространенные эмпирические потенциалы межатомного взаимодействия и принципы расчета первопринципных потенциалов.

4. Обменное взаимодействие и его роль.

Рассмотреть природу обменного взаимодействия и выяснить, к каким макроскопическим, обнаруживаемым даже без приборов, явлениям оно приводит.

5. Эффективность методов Монте-Карло.

Рассмотреть погрешности вычислений определенных интегралов и установить критерии эффективности методов Монте-Карло для одномерных и многомерных интегралов.

Список рекомендуемой литературы

1. Гулд Х. Тобочник Я. Компьютерное моделирование в физике. — М.: Мир, 1990.

2. Гегузин Я.Е. Живой кристалл. — М.: Наука, 1991.

3. Соболь И.М. Метод Монте-Карло. — М.: Наука, — 1985.

4. Сборник «Эксперимент на дисплее» под ред. А.А. Мигдала — М.: Наука, 1985.

5. Эфрос А.Л. Физика и геометрия беспорядка. —М., Наука, 1982

6. Википедия http://ru.wikipedia.org

7. Журнал «Успехи физических наук» (http://www.ufn.ru)

8. Гуревич А.Г. «Физика твердого тела», СПб, 2004г.

9. Физическая мезомеханика и компьютерное конструирование материалов. Отв. ред. Панин В.Е. —Новосибирск, Наука, 1995