Как получается дифракционная картина?
Решетка кристалла обладает симметрией, которая проявляется в симметрии его свойств. Так, если в монокристалле с кубической решеткой измерять свойства вдоль ребра кубика и его диагонали, они окажутся разными, так как атомы в этих направлениях располагаются на разных расстояниях. Симметрия решетки кристалла проявляется и во внешней форме ограненных природных кристаллов, и в симметрии дифракционной картины.
На рисунке 2 приведена рентгенограмма, полученная от монокристалла каменной соли. Рентгеновский луч был направлен параллельно ребру кубической ячейки NaCl. Это направление в решетке является осью симметрии 4-го порядка: при полном обороте вокруг этой оси кристалл совмещается сам с собой 4 раза. Видно, что эта симметрия сохранилась и в рентгенограмме. Направляя рентгеновский луч вдоль разных направлений в монокристалле и анализируя вид дифракционной картины, можно полностью выявить симметрию кристаллической решетки.

Рисунок 2. Схема кристаллической решетки NaCl и дифракционная картина от монокристалла NaCl.
Для понимания принципов получения дифракционной картины на кристалле удобно представить его решетку как совокупность параллельных друг другу плоскостей одинаково заполненных атомами и отстоящих друг от друга на одинаковые расстояния d. Такие плоскости называются семейством. В решетке можно найти множество самых разных семейств плоскостей с различными межплоскостными расстояниями (см. рис.3). Поскольку решетки разных кристаллов отличаются друг от друга размерами и формой, каждому кристаллу соответствует свой, только ему присущий набор межплоскостных расстояний.

Рисунок 3. Семейства плоскостей в решетке кристалла.
Из оптики известно, что при взаимодействии с одной плоскостью, излучение отражается под тем же углом, под которым было направлено на плоскость, а падающий и отраженный лучи лежат в одной плоскости с нормалью к отражающей плоскости. Рентгеновское излучение проникает в материал на значительную глубину, встречая на своем пути десятки тысяч атомных плоскостей.
Для того чтобы лучи, отраженные каждой плоскостью, не гасили друг друга, а складывались и составляли дифрагированный луч, необходимо, чтобы разность хода лучей, отраженных любыми двумя плоскостями, была равна целому числу длин волн излучения: Δl = nλ
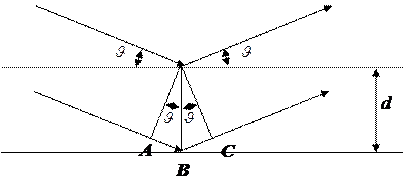
Рисунок 4. Разность хода лучей, рассеянных двумя соседними плоскостями кристалла
Если рентгеновский луч падает на плоскости под углом θ, разность хода лучей Δl, как видно из рисунка 4, равна АВ+ВС =2dsinθ. Тогда условие дифракции будет записано в виде: 2dsinθ = nλ. То есть, отражение лучей с длиной волны λ от какого-либо семейства плоскостей кристалла возможно только в том случае, когда излучение падает на плоскости под строго определенным углом, зависящим от λ и d. Получая отражения от разных плоскостей кристалла и измеряя углы дифракции, можно, зная длину волны использованного излучения, рассчитать межплоскостные расстояния. А так как каждому веществу соответствует свой набор межплоскостных расстояний, по ряду величин d,определенных экспериментально, можно узнать, какое именно вещество исследовалось.
Дифракционная картина поликристалла является наложением дифракционных картин от множества кристалликов, произвольно ориентированных друг относительно друга. Лучи, отраженные одинаковыми плоскостями в разных кристалликах, будут располагаться под одним углом к падающему пучку и образуют в пространстве конус. Разным плоскостям соответствуют разные дифракционные конусы. Такую дифракционную картину сложно зарегистрировать на фотопленку. Для съемки рентгенограмм поликристаллических веществ используют специальный прибор – дифрактометр. Общий вид прибора показан на рисунке 5. А на рисунке 6 приведена типичная дифракционная картина, полученная от образца порошка меди.

Рисунок 5. Общий вид рентгеновского дифрактометра ДРОН-7
Каждая линия под своим определенным углом на дифрактограмме рис.6 соответствует отражениям от плоскостей с одинаковым межплоскостным расстоянием d в разных зернах поликристалла.
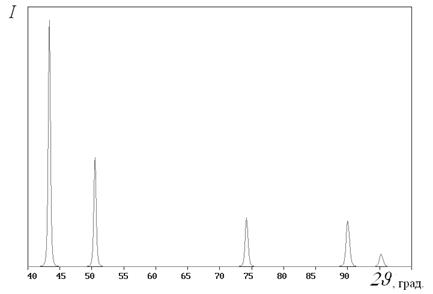
Рисунок 6. Участок дифрактограммы порошка меди.
Дата добавления: 2015-02-07; просмотров: 3481;
