Дифракционная решетка как спектральный прибор

Для волн разной длины 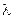положения максимумов нулевого порядка совпадают. Положения максимумов первого, второго и т.д. порядков различны: чем больше 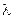, тем больше соответствующие этим максимумам углы дифракции .

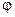Если на дифракционную решетку падает немонохроматический свет {например, белый), то в плоскости экрана получается ряд цветных изображения цели, расположенных в порядке возрастания длин волн. На месте нулевого максимума, где сходятся все длины волн, будет изображение щели в белом свете, а по обе стороны от него будет ряд спектров, для которых 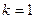(спектр первого порядка), 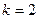(спектр второго порядка) и т.д. Если известен период дифракционной решетки, то ее можно использовать для определения длины световой волны.

6. Дисперсия в разрешающая способность дифракционной решетки

Угловая дисперсия 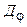спектрального прибора (дифракционной решетки) определяется отношением углового расстояния 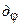между двумя близкими спектральными линиями к разности их длин волн :

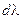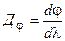(11)

Из формулы (9) для дисперсии дифракционной решетки имеем

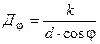(12)

при малых углах (φ<10º) 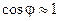и

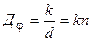(13)

т.е. спектр равномерно растянут при всех длинах волн.

Разрешающая способность 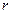спектрального прибора численно равна отношению длины волны 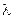к той минимальной разности длин волн 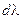, при которой еще можно раздельно видеть две монохроматические спектральные линии. Релей предложил считать спектральные линии разрешенными, если середина одного максимума совпадает с краем другого (рис.12).

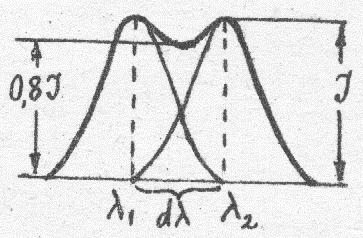
Рис.12

В этом случае минимум между линиями составляет 80% от двух равных максимумов. Простой расчет разрешающей способности с применением условия Релея приводит к выражению 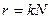, где 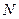– число щелей решетки.