Дифракционная решетка

Одним из наиболее распространенных приборов для получения спектров с помощью дифракции является дифракционная решетка. Дифракционные решетки бывают прозрачные и отражательные. Первые представляют собой последовательность параллельных щелей равной ширины, разделенных равными по ширине непрозрачными промежутками. В отражательных решетках щели заменены зеркальными полосками. Чаще применяются прозрачные решетки. На рис.8 схематически изображена такая решетка. Ширина щели равна , ширина непрозрачного участка – . 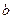Сумма 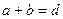называется периодом, или постоянной дифракционной решетки. Постоянная решетки 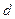связана с числом штрихов на единицу длины (на 1мм) соотношением .

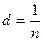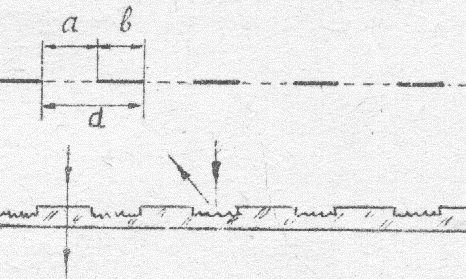
Рис.8

Рассмотрим плоскую монохроматическую волну, падающую нормально на решетку. За решеткой расположим собирающую линзу, а в ее фокальной плоскости – непрозрачный экран Э (рис.9).

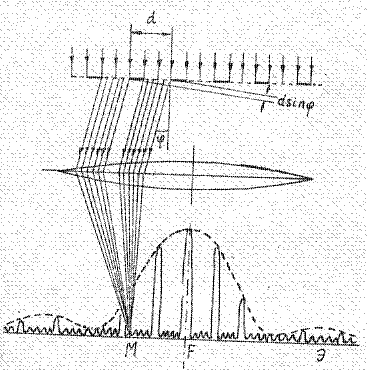
Рис.9

Каждая из щелей дает на экране дифракционную картину, показанную на рис.9 пунктирной линией. Картина, получаемая в результате интерференции лучей от многих щелей, является более сложной ( на рис. 9 сплошная линия). Объясним образование такой картины. Линза собирает параллельные лучи, идущие от всех щелей под углом 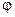к главной оптической оси линзы в одну и ту же точку М на экране (на рис.9 показаны такие лучи от двух соседних щелей). Амплитуда колебаний, создаваемых в точке М каждой щелью в отдельности, будут одинаковыми. Рассмотрим сначала картину, получаемую на центральной линии экрана, проходящей через главный фокус линзы Р. Для этой линии 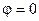, и лучи, идущие от всех щелей, сходятся без дополнительной разности фаз. т.е. в одной фазе. При этом амплитуды их просто складываются: в случае N одинаковых щелей амплитуда суммарного колебания будет в N раз больше, а интенсивность в 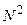раз больше, чем в случае одной щели. Теперь представим себе картину, которую дают лучи, идущие под углом 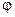к первоначальному направлению лучей. Эти лучи (см. рис.9) сходятся в точке М, пройдя разные пути и имея, следовательно, разные фазы колебаний. Возьмем две соседние щели. Лучи, идущие от соответственных точек обеих щелей, имеют одну и ту же разность хода: 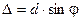и приходят в точку М со сдвигом фаз 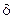, равным

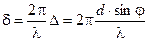(7)

Очевидно, такой сдвиг фазы будет между колебаниями, приходящими от любой пары соседних щелей. Резкое возрастание амплитуды наблюдается только при тех углах 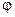, при которых достигается разность фаз 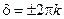, т.е. когда векторы амплитуд колебаний от всех щелей направлены одинаково (см. векторную диаграмму на рис.10). Из формулы (7) следует, что это условие соответствует разности хода

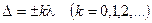(8)

или

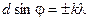(9)

где 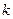– порядковый номер дифракционного максимума. Эту формулу называют также основной формулой дифракционной решетки. Для анализа результатов интерференции дифрагированных лучей используем векторную диаграмму. Результирующая амплитуда равна

,

где 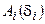– амплитуда колебаний от 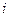-й щели, имеющих разность фаз 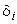. По модулю 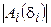одинаковы и равны 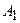. Как отмечалось. при выполнении условия (8) все векторы 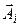совпадают по направлению, и возникает главный максимум. При большом количестве щелей ширина главных максимумов становится малой. Действительно, если мы сдвинемся на малый угол 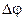в сторону от главного максимума, то условие 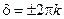нарушится, и между векторами 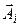появится дополнительный сдвиг фаз 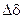, равный

(10)

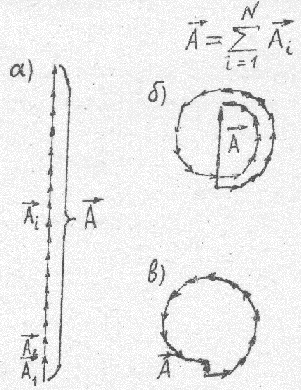
Рис.10

Тогда вместо прямой (см. рис.10а) при сложении амплитуд получится многоугольник. Каждый вектор 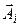будет повернут относительно предыдущего 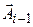на один и тот же угол 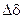. Амплитуда 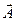результирующего колебания является замыкающей многоугольника из векторов 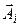(см.рис.10 б и в), Положение замыкающего вектора зависит от числа щелей 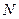и угла 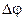. Если число щелей велико, то многоугольник даже при малом сдвиге фаз 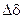несколько раз обернется вокруг центральной точки О. Если суммарный угол сдвига фаз при обходе многоугольника 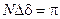, то многоугольник замкнется (см.рис.10 б), и результирующая амплитуда 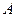будет иметь максимальное значение. При 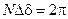результирующая амплитуда имеет минимальное значение (см. рис.10 в). С увеличением угла 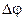изменяется и 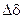, поэтому при отклонении от главного максимума суммарная амплитуда 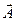возрастает и убывает. Однако величина возникающих побочных максимумов и минимумов будет небольшой (близкой к 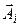), пока мы не дойдем до следующего главного максимума, определяемого условием (9).

Таким образом, интерференционная картина, даваемая дифракционной решеткой, состоит из интенсивных узких главных максимумов, между которыми расположены серии небольших побочных максимумов, интенсивности которых тем меньше, чем больше общее число щелей 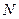(рис.11).

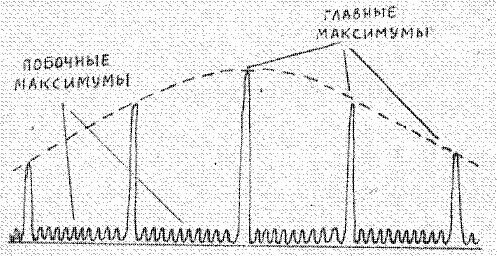
Рис.11

Из формулы (9) следует, что для данной волны 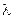может наблюдаться несколько главных максимумов. В направлении, соответствующем 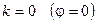, наблюдается максимум нулевого порядка, при 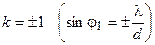– два главных максимума первого порядка, расположенных симметрично по обеим сторонам максимума нулевого порядка. Далее следуют попарно максимумы второго ( 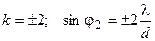), третьего ( 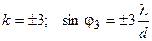) и т.д. порядков. Распределение интенсивности главных максимумов определяется видом распределения интенсивности дифракционной картины от одной щели (см. рис.9).