ДВИЖУЩАЯ СИЛА МАССООБМЕННЫХ ПРОЦЕССОВ
Движущая сила массообменных процессов, как было сказано, определяется степенью отклонения от равновесия, которое вычисляется как разность между рабочей и равновесной концентрациями или, наоборот, равновесной и рабочей в зависимости от того, какие значения из них больше. Движущую силу можно выразить через концентрации распределяемого вещества в фазе G через у или в фазе L через Х.
Различают локальные движущие силы, вычисленные для массообменного процесса, протекающего на бесконечно малой площади контакта фаз, и движущие силы для всего процесса массообмена в пределах изменения концентраций от начальных до конечных.
Локальные движущие силы изменяются с изменением концентраций, поэтому для всего процесса массообмена вычисляют средние движущие силы.
Выражение и значение средней движущей силы зависят от вида уравнения равновесия.
Рассмотрим определение средней движущей силы, когда линия равновесия определяется уравнением кривой (рис. 12.6) 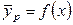 в противоточном массообменном аппарате при условии
в противоточном массообменном аппарате при условии 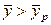 .
.
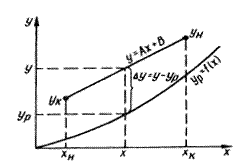
Рис. 12.6. Изображение рабочей и равновесной линий в координатах y-x
Примем, что расходы фаз G и L постоянны, коэффициенты массопередачи 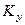 и
и 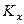 не меняются по длине аппарата,
не меняются по длине аппарата, 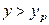 и перенос вещества происходит из фазы G в фазу L.
и перенос вещества происходит из фазы G в фазу L.
Для элемента поверхности на основании уравнения материального баланса (12.5) можно записать 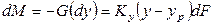 .
.
Разделяя переменные 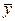 и F и интегрируя это выражение в пределах изменения концентрации от
и F и интегрируя это выражение в пределах изменения концентрации от 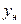 до
до 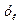 (см. рис. 12.1) и поверхности контакта фаз от 0 до F, получим
(см. рис. 12.1) и поверхности контакта фаз от 0 до F, получим
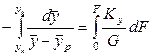 , (12.39)
, (12.39)
откуда
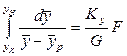 . (12.40)
. (12.40)
Согласно уравнению материального баланса (12.6) количество вещества, перешедшего из фазы G в фазу L, равно 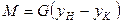 . Подставим G из последнего выражения в уравнение (12.40)
. Подставим G из последнего выражения в уравнение (12.40)
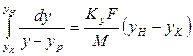 ,
,
откуда
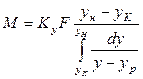 ; (12.41)
; (12.41)
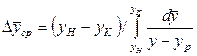 . (12.42)
. (12.42)
Аналогично можно определить среднюю движущую силу в концентрациях 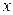 в фазе L
в фазе L
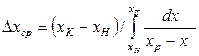 . (12.43)
. (12.43)
Интеграл в знаменателе уравнений (12.42) и (12.43) называется числом единиц переноса 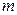 :
:
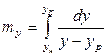 ; (12.44)
; (12.44)
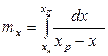 . (12.45)
. (12.45)
Из уравнений (12.41), (12.42), (12.44) и (12.45) находят соотношения между средней движущей силой и числом единиц переноса:
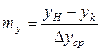 . (12.46)
. (12.46)
Сопоставляя уравнение (12.41) с основным уравнением массопередачи (12.2), найдем выражения средних движущих сил массопередачи
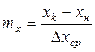 . (12.47)
. (12.47)
Из уравнений (12.46) и (12.47) следует, что число единиц переноса обратно пропорционально средней движущей силе процесса.
Из уравнений (12.46) и (12.47) также следует, что число единиц переноса характеризует изменение рабочих концентраций на единицу движущей силы.
В уравнениях (12.42) и (12.43) знаменатель дробей находят графическим интегрированием. Так, например, в пределах концентраций 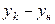 , через определенные интервалы для ряда значений у находят соответствующие им величины х,
, через определенные интервалы для ряда значений у находят соответствующие им величины х, 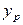 ,
, 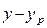 и
и 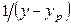 .
.
На диаграмме в координатах 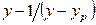 строят кривую, как показано на рис. 12.7. Площадь под кривой, ограниченная ординатами
строят кривую, как показано на рис. 12.7. Площадь под кривой, ограниченная ординатами 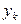 и
и 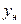 умноженная на масштаб диаграммы
умноженная на масштаб диаграммы 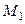 и
и 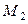 , дает искомый интеграл
, дает искомый интеграл
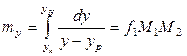 . (12.48)
. (12.48)
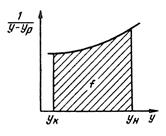
Рис. 12.7. К определению числа единиц переноса графическим интегрированием
Ниже будет показано, что число единиц переноса используют для расчета высоты массообменных аппаратов, особенно когда поверхность контакта фаз трудно определить.
В частных случаях, например при массопередаче в разбавленных растворах (адсорбция, экстракция), а также при расчете массообменных аппаратов, когда для упрощения расчетов аппроксимируют линию равновесия прямой, средняя движущая сила массопередачи определяется, как и при расчете теплообменных аппаратов, как средняя логарифмическая или средняя арифметическая величина из движущих сил на входе и выходе из аппарата.
Рассмотрим расчет средних движущих сил при различных схемах взаимодействия потоков.
На рис. 12.8,а приведена общая схема изменения концентраций при противоточном взаимодействии потоков.
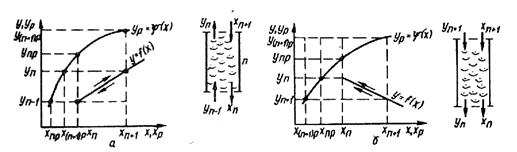
Рис. 12.8. Схемы массообмена и условия отсчета движущих сил:
а – при противотоке; б – при прямотоке
В этом случае средние движущие силы в  - м элементе аппарата определяются так:
- м элементе аппарата определяются так:
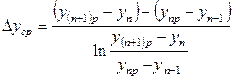 ; (12.49)
; (12.49)
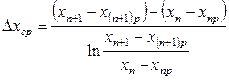 . (12.50)
. (12.50)
В случае прямотока (рис. 12.8, б)
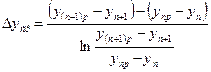 ; (12.51)
; (12.51)
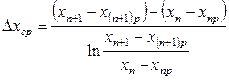 . (12.52)
. (12.52)
При расчете движущей силы при перекрестном токе взаимодействующих фаз принимают в большинстве случаев одну из схем изменения концентраций фаз в аппарате, а именно: обе фазы на элементе аппарата идеально перемешаны; газ (пар) идеально перемешан, а в фазе, протекающей через элемент аппарата, концентрация меняется линейно; фаза, перетекающая через элемент аппарата, идеально перемешана, а в газе (паре), пронизывающем перетекающий поток, концентрация меняется линейно.
Схема массообмена на элементе аппарата и условия отсчета движущих ил приведены на рис. 12.9.
На 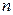 - й элемент поступает фаза концентрацией
- й элемент поступает фаза концентрацией 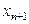 . В результате массообмена с поступающим с нижележащего элемента газом (паром) с концентрацией
. В результате массообмена с поступающим с нижележащего элемента газом (паром) с концентрацией 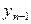 концентрация в жидкой фазе изменяется до конечной, равной
концентрация в жидкой фазе изменяется до конечной, равной 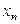 , а концентрация в паре изменяется до
, а концентрация в паре изменяется до 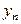 .
.
В случае, когда обе фазы на элементе аппарата идеально перемешаны, средняя движущая сила определяется так:
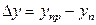 ; (12.53)
; (12.53)
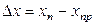 .
.
Условия отсчета движущей силы для случая, когда жидкая фаза идеально перемешана на элементе и имеет концентрацию 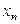 , равную концентрации на выходе, а газ (пар) линейно меняет концентрацию от
, равную концентрации на выходе, а газ (пар) линейно меняет концентрацию от 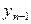 до
до 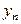 , представлены на рис. 12.9.
, представлены на рис. 12.9.
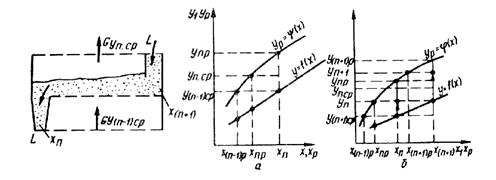
Рис. 12.9. Схема массообмена и условия отсчета движущих сил при перекрестном токе:
а – жидкая фаза идеально перемешана, а пар (газ) идеально вытесняется в слое; б – обе фазы идеально перемешаны
Следует отметить, что эта схема изменения концентраций в фазах соответствует процессу в аппаратах перекрестного тока небольших диаметров.
На таком представлении о характере взаимодействия фаз основан ряд методов расчета размеров аппаратов. В этом случае движущие силы определяются так:
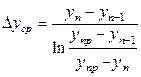 ;
; 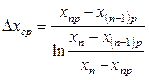 . (12.54)
. (12.54)
Для случая идеального вытеснения потоков средние движущие силы в аппарате (рис. 12.9,б) будут определяться как средние логарифмические из движущих сил на входе потока и на выходе из аппарата. Граничные локальные движущие силы в аппарате при линейном изменении концентраций в паре (газе) определяются уравнениями. Среднюю движущую силу с учетом выражений (12.54) можно получить в виде
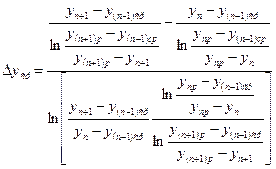 ; (12.55)
; (12.55)
Расчет движущей силы из принятых условных схем взаимодействия потоков приводит, как правило, к погрешностям в определении площади рабочей поверхности аппарата.
Все реальные аппараты, как было отмечено выше, в большинстве случаев относятся по гидродинамической характеристике к аппаратам промежуточного типа, в которых движущая сила зависит от распределения концентраций и температур в рабочей зоне аппарата.
Общим для рассмотренных выше схем изменения концентраций в фазах является то, что ни одна из них не учитывает реальной гидродинамической обстановки в аппарате.
Действительную движущую силу можно определить на основании гидродинамических моделей и экспериментальных данных по перемешиванию фаз на контактном устройстве.
Коэффициент использования движущей силы в прямо- и противоточных аппаратах
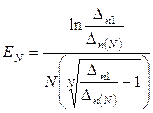 , (12.56)
, (12.56)
где: 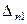 ,
, 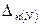 - движущие силы на входе и выходе из
- движущие силы на входе и выходе из 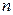 -го контактного устройства.
-го контактного устройства.
Для аппаратов перекрестного тока соответственно получено выражение
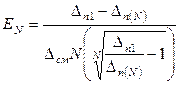 . (12.57)
. (12.57)
Из уравнения (12.57) по фазе L, например, при 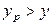 получим
получим
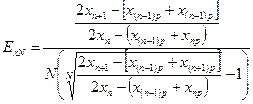 . (12.58)
. (12.58)
Из последнего уравнения можно получить выражение, удобное для расчетов,
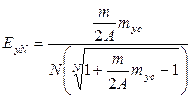 . (12.59)
. (12.59)
где: 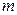 и А — тангенсы углов наклона равновесной и рабочей линий;
и А — тангенсы углов наклона равновесной и рабочей линий; 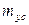 - число единиц переноса по фазе G, вычисленное при условии идеального перемешивания газовой (паровой) фазы; N — количество псевдосекций.
- число единиц переноса по фазе G, вычисленное при условии идеального перемешивания газовой (паровой) фазы; N — количество псевдосекций.
В некоторых массообменных аппаратах, например в насадочных, тарельчатых, площадь поверхности фазового контакта трудно определить. В этих случаях для их расчета используют модифицированные уравнения массопередачи.
Площадь поверхности фазового контакта в таких аппаратах
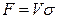 ,
,
где: 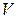 - объем аппарата,
- объем аппарата, 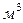 ;
; 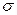 - удельная поверхность фазового контакта,
- удельная поверхность фазового контакта, 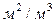 .
.
Подставляя величину F в уравнение массопередачи (12.4), получим
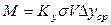 . (12.60)
. (12.60)
Величины 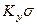 и
и 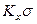 называют объемными коэффициентами массопередачи, соответственно
называют объемными коэффициентами массопередачи, соответственно 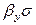 и
и 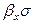 - объемными коэффициентами массоотдачи.
- объемными коэффициентами массоотдачи.
Из уравнения (12.60) получают
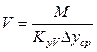 , или
, или 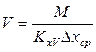 ,
,
где: 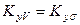 и
и 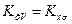 - объемные коэффициенты массопередачи.
- объемные коэффициенты массопередачи.
Представив 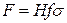 , можно из (12.41) определить высоту массообменного аппарата, имея в виду, что
, можно из (12.41) определить высоту массообменного аппарата, имея в виду, что 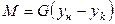 :
:
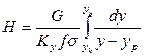 , (12.61)
, (12.61)
где: 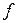 - площадь поперечного сечения аппарата,
- площадь поперечного сечения аппарата, 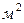 .
.
Величина 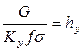 представляет собой высоту аппарата, эквивалентную единице переноса (ВЕП), и измеряется в единицах высоты. В случае выражения числа единиц переноса в концентрациях х эта величина равна
представляет собой высоту аппарата, эквивалентную единице переноса (ВЕП), и измеряется в единицах высоты. В случае выражения числа единиц переноса в концентрациях х эта величина равна 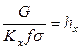 . С учетом этого модифицированные уравнения массопередачи принимают вид
. С учетом этого модифицированные уравнения массопередачи принимают вид
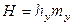 ;
;
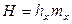 . (12.62)
. (12.62)
Сопоставление полученных уравнений (12.62) с основным уравнением массопередачи показывает, что высота, эквивалентная единице переноса 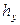 или
или 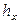 , обратно пропорциональна объемному коэффициенту массопередачи.
, обратно пропорциональна объемному коэффициенту массопередачи.
Таким образом, чем выше коэффициент массопередачи, тем ниже величина ВЕП.
Дата добавления: 2015-03-14; просмотров: 3102;
