ОСНОВНЫЕ ЗАКОНЫ МАССОПЕРЕДАЧИ

В процессах массопередачи следует различать несколько случаев массообмена: между потоком газа или пара и потоком жидкости; между потоками жидкости; между потоками жидкости и твердой фазой; между потоками газа или пара и твердой фазой.

Основными законами массопередачи являются закон молекулярной диффузии (первый закон Фика), закон массоотдачи (закон Ньютона - Щукарева) и закон массопроводности.

Закон молекулярной диффузии (первый закон Фика), основанный на том, что диффузия в газах и растворах жидкостей происходит в результате хаотического движения молекул, приводящего к переносу молекул распределяемого вещества из зоны высоких концентраций в зону низких концентраций, гласит: количество вещества, перенесенного путем диффузии, пропорционально градиенту концентраций, площади, перпендикулярной направлению диффузионного потока, и продолжительности процесса:

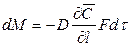, (12.9)

где: dM – количество вещества, перенесённого путём диффузии; D – коэффициент пропорциональности, или коэффициент диффузии; 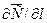- градиент концентрации в направлении диффузии; F – элементарная площадка, через которую происходит диффузия; dτ – продолжительность диффузии.

Коэффициент диффузии показывает, какое количество вещества диффундирует через поверхность в 1 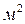в течение 1 ч при разности концентраций на расстоянии 1 м, равной единице.

Знак «минус» в правой части уравнения показывает, что при молекулярной диффузии концентрация убывает.

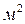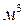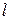Если единицы измерений [М] = [кг], [Р] = [ ], [τ] = [ч], [С] = [кг/ ] и [ ]=[м], то размерность коэффициента диффузии определится из уравнения (12.9):

.

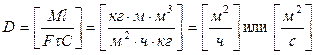Значения коэффициента диффузии обычно берут из справочников или находят по следующим формулам:

для газов

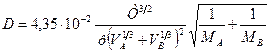; (12.10)

для жидкостей

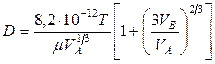, (12.11)

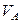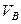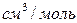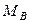где: Т – температура, К; - давление, Па; и - мольные объемы взаимодействующих веществ, ; и - молекулярные массы веществ, кг/кмоль; 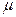- динамическая вязкость, 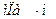, А и В - опытные константы, зависящие от природы вещества.

Коэффициенты диффузии зависят от агрегатного состояния систем. Для газов коэффициенты диффузии имеют значения (0,1... 1,0)10^-4 . Они примерно на четыре порядка выше, чем для жидкостей. С увеличением температуры коэффициенты диффузии возрастают, а с повышением давления уменьшаются.

Коэффициенты диффузии в газах почти не зависят от концентрации, в то время как коэффициенты диффузии в жидкостях изменяются с изменением концентрации диффундирующего вещества.

Дифференциальное уравнение молекулярной диффузии (второй закон Фика) получают, рассмотрев материальный баланс по распределяемому веществу для элементарного параллелепипеда, выделенного мысленно в потоке одной из фаз (рис. 12.3).

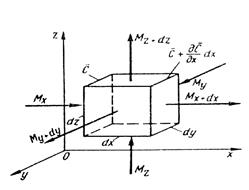
Рис. 12.3. К выводу дифференциального уравнения молекулярной диффузии

Пусть через этот элементарный параллелепипед за счет молекулярной диффузии перемещается вещество. Если через гран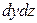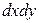и , и 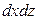проходят количества вещества, соответственно равные , , 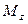, то через противоположные грани выходят количества вещества , , 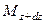, т. е. элементарный объем параллелепипеда приобретает диффундирующее вещество в количестве 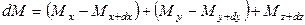. При этом концентрация вещества повышается на 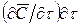. Согласно основному закону молекулярной диффузии (первый закон Фика)

;

.

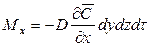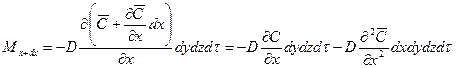и, следовательно,

.

Аналогично найдем разности между количествами вещества, прошедшего через другие противоположные грани параллелепипеда.

Общее количество приобретенного вещества

. (12.12)

Это же количество вещества можно найти умножением объема параллелепипеда на изменение концентрации диффундирующего вещества за время :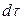

. (12.13)

Приравнивая уравнения (12.12) и (12.13), получим дифференциальное уравнение молекулярной диффузии

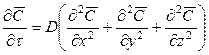. (12.14)

Основной закон массоотдачи, который является аналогом закона Ньютона, был установлен русским ученым Щукаревым при изучении растворения твердых тел. Этот закон формулируется так: количество вещества, перенесенного потоком от поверхности раздела фаз (контакта фаз) в воспринимающую фазу или в обратном направлении, прямо пропорционально разности концентраций у поверхности контакта фаз и в ядре потока воспринимающей фазы, площади поверхности контакта фаз и продолжительности процесса.

Согласно теории диффузионного пограничного слоя распределяемое вещество переносится из ядра потока жидкости к поверхности раздела фаз непосредственно конвективными потоками жидкости и молекулярной диффузией. В рассматриваемой системе (рис. 12.4) различают ядро потока и приграничный диффузионный слой. В ядре перенос вещества осуществляется преимущественно потоками жидкости или газа. В условиях турбулентного течения потоков концентрация распределяемого вещества в данном сечении в условиях стационарного режима сохраняется постоянной. По мере приближения к пограничному диффузионному слою турбулентный перенос снижается и начинает увеличиваться перенос за счет молекулярной диффузии. При этом появляется градиент концентрации распределяемого вещества, растущий по мере приближения к границе. Таким образом, область пограничного диффузионного слоя — это область появления и роста градиента концентрации, область увеличения влияния скорости молекулярной диффузии на общую скорость массопередачи.

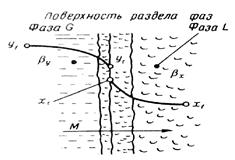
Рис.12.4. К выводу уравнения массоотдачи

Примем, что распределяемое вещество М переходит из фазы G, в которой его концентрация выше равновесной, в фазу L.

Если концентрации вещества в ядрах фаз принять равным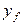и и 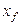, а концентрации на поверхности раздела фаз — соответственно 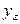и , , то процесс массоотдачи вещества из ядра фазы G к поверхности раздела фаз и от поверхности раздела фаз в ядро фазы L можно записать так:

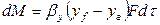; (12.15)

,

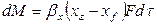где: 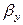, 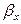- коэффициенты массоотдачи, характеризующие перенос вещества конвективными и диффузионными потоками одновременно; концентраци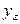и и предполагаются равными равновесным, т. е. и .

Размерность коэффициента массоотдачи .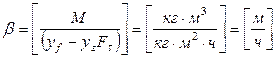

Коэффициент массоотдачи показывает, какое количество вещества передается от поверхности контакта фаз площадью в 1 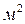в ядро воспринимающей фазы или в обратном направлении в течение единицы времени при разности движущих сил, равной единице.

По физическому смыслу коэффициенты массоотдачи отличаются от коэффициентов массопередачи, но выражаются в одинаковых единицах.

Для установившегося процесса 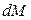выражает количество вещества, перенесенного от поверхности контакта фаз в ядро или из ядра потока к ее поверхности в единицу времени.

Для этого случая уравнение (12.15) перепишется так:

.

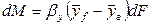Если 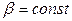для всей поверхности контакта фаз,

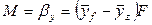. (12.16)

Если рассмотреть вновь элементарный объем фазы (см. рис. 12.3), перемещающийся в пограничном слое, то можно утверждать, что концентрация распределяемого вещества в нем меняется не только за счет молекулярной диффузии, но также и за счет турбулентного переноса его. В этом случае концентрация распределяемого вещества будет функцией не только координат и времени, как в случае только молекулярной диффузии, но и скорости перемещения.

Соответственно этому изменение концентрации G выразим через субстанциональную производную:

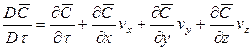. (12.17)

В этом уравнении сумма членов 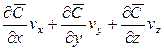характеризует конвективное изменение концентрации, а 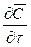- локальное.

Увеличение количества распределяемого вещества за счет молекулярной диффузии определяется уравнением (12.14). Приравнивая уравнение (12.17) к (12.14) и заменяя локальное изменение концентрации 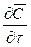на полное 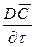в (12.17), получим дифференциальное уравнение конвективной диффузии

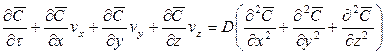. (12.18)

Для полного математического описания процесса это уравнение должно быть дополнено уравнением, характеризующим условие на границе раздела фаз.

Количество вещества, передаваемого из фазы в фазу у границы, определяется основным законом конвективной диффузии (12.15). У поверхности раздела фаз вещество переходит из фазы в фазу, как было установлено выше, за счет молекулярной диффузии [см. уравнение (12.9)]. Приравнивая эти уравнения, получим

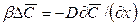, (12.19)

где: 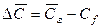- движущая сила процесса.

Уравнение (12.19) характеризует условие массообмена на границе фазы и дополняет уравнение (12.18), являясь вместе с ним математическим описанием процесса конвективной диффузии.

Критериальные уравнения конвективной диффузии получают из уравнений (12.18) и (12.19).

Для получения диффузионных критериев, подобия воспользуемся методами теории подобия. Из уравнения (12.19) получим безразмерный комплекс 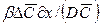, из которого после сокращения получают диффузионный критерий Нуссельта

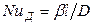, (12.20)

который характеризует условия на границе рассматриваемой фазы, т. е. выражает отношение интенсивности переноса вещества в ядре фазы конвективной диффузией к интенсивности переноса в диффузионном слое, где интенсивность переноса определяется молекулярной диффузией D.

Из дифференциального уравнения конвективной диффузии (12.18), разделив все члены на , получим безразмерные комплексы

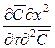и

и соответственно диффузионный критерий Фурье

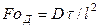(12.21)

и диффузионный критерий Пекле

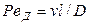. (12.22)

Критерий 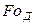характеризует изменение скорости потока диффундирующей массы во времени и используется для характеристики нестационарных процессов диффузии. Преобразуем критерий 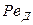и представим его в виде произведения

.

Диффузионный критерий Прандтля 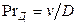характеризует подобие полей физических величин и определяется только физическими свойствами вещества. Найдя критерии подобия, характеризующие явление массообмена, запишем общее критериальное уравнение конвективной диффузии

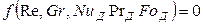. (12.23)

Критерий Нуссельта в этом уравнении является определяемым в отличие от других критериев, которые являются определяющими, т. е. составленными целиком из параметров, входящих в условие однозначности. Коэффициент массоотдачи, входящий в критерий Нуссельта, не входит в условие однозначности и является искомой величиной.

В явном виде уравнение (12.23) перепишется так:

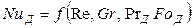. (12.24)

Критерий Грасгофа в этом уравнении характеризует конвективную диффузию в условиях естественной конвекции.

В случае стационарных процессов из общего критериального уравнения исключается критерий Фурье и оно приобретает вид

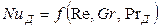. (12.25)

При вынужденном движении можно пренебречь естественной конвекцией. В этом случае из уравнения (12.25) выпадает критерий Грасгофа и уравнение приобретает вид

. (12.26)

Конкретные критериальные уравнения приводятся в соответствующих главах этой части.

По значениям критерия Нуссельта, найденным по критериальным уравнениям, определяют коэффициент массоотдачи

. (12.27)

Между переносом теплоты, массы и механической энергии существует, как отмечалось ранее, аналогия, эти процессы описываются однотипными дифференциальными уравнениями.

При рассмотрении движения потока жидкости в трубе различают пограничный слой и ядро потока. В ядре турбулентного потока происходит выравнивание скоростей по нормали к вектору скорости, в пограничном же слое происходит резкое изменение скорости потока до нуля. Такое же выравнивание температур и концентраций происходит в процессах тепло- и массопередачи. Таким образом, имеет место аналогия между этими процессами.

Исходя из этой аналогии, можно приближенно определять коэффициенты массоотдачи по данным о трении жидкостного потока или о скорости переноса теплоты.

На основании гидродинамической аналогии можно определить отношение коэффициента массоотдачи к средней скорости потока 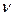, которое представляет собой безразмерную величину и носит название диффузионного критерия Стантона

.

Критерий Стантона характеризует подобие полей концентраций и скоростей при массоотдаче в турбулентных потоках.

Существует связь между коэффициентом массопередачи и коэффициентами массоотдачи. Рассмотрим процесс массопередачи при переходе распределяемого вещества из фазы G в фазу L при условии линейных зависимостей между рабочими и равновесными концентрациями (см. рис. 12.4). Примем, что на границе раздела фаз достигается равновесие.

Количество вещества, перемещающегося из фазы G к поверхности на границе раздела фаз, может быть определено по уравнению

,

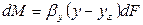где: 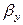- коэффициент массоотдачи для фазы, G.

Количество распределяемого вещества, перемещающегося от элемента поверхности в фазу L, может быть вычислено также по фазе L по уравнению (12.15). В этом случае движущую силу следует выразить разностью :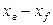

,

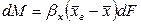где: 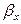- коэффициент массоотдачи для фазы L.

Так как известна равновесная зависимость 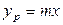, концентрацию 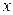в фазе L можно выразить через равновесную в фазе G:

.

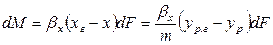Тогда

.

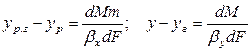Сложим левые и правые части этих уравнений

,

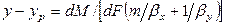так как .

Из основного уравнения массопередачи (12.4) получим

.

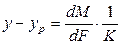Приравнивая правые части уравнения, получим

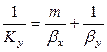или 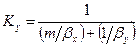. (12.28)

Рассуждая аналогично, для фазы L будем иметь

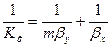или 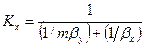. (12.29)

Левые части этих уравнений представляют собой общее диффузионное сопротивление переносу, а их правые части — сумму диффузионных сопротивлений массоотдаче в фазах. Зависимости (12.28) и (12.29) являются поэтому уравнениями аддитивности фазовых сопротивлений.

Коэффициенты 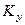и 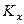связаны соотношением 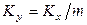. Числовые значения коэффициентов массопередачи определяются значениями коэффициентов массоотдачи и углом наклона равновесной линии. Коэффициенты массоотдачи определяют по критериальным уравнениям.