МАССОПЕРЕДАЧА С ТВЕРДОЙ ФАЗОЙ

К этим процессам относятся экстракция из твердых пористых материалов (выщелачивание), сушка и адсорбция.

Массоперенос в твердом пористом материале представляет собой неустановившийся процесс.

Перенос вещества из твердого капиллярно-пористого тела через границу раздела фаз в газовую (паровую) среду (сушка), в жидкую (экстракция) или из газовой (паровой) среды в твердое тело (адсорбция) происходит при наличии градиента потенциала переноса в направлении достижения равновесия.

На перенос вещества значительное влияние оказывает его структура. Твердое пористое тело представляет собой систему со сложными многообразными геометрическими характеристиками, главными из которых являются пористость, полидисперсность, распределение пор по размерам, форма капилляров.

В зависимости от капиллярно-пористой структуры твердые материалы классифицированы в порядке уменьшения величины критического диаметра пор, которому соответствуют усложнение внутренней структуры твердого тела и увеличение внутридиффузионного сопротивления, на широкопористые ( 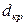до 100 нм), среднепористые и материалы с ультрамикропорами.

В общем случае перенос вещества внутри пористого твердого тела осуществляется как в паровой, так и в жидкой фазе. В случае десорбции влаги при небольшой влажности материала влага перемещается в основном за счет молекулярного переноса пара. При большой влажности материала перемещение жидкости и пара обусловлено явлениями с различными механизмами переноса: капиллярными, осмотическими, термокапиллярными, гравитационными потоками газовой (паровой) фазы.

Значение каждого из перечисленных механизмов переноса зависит от капиллярно-пористой структуры твердого тела и режима проведения процесса.

Массоперенос в системе с твердой фазой рассмотрим на примере десорбции влаги из твердого тела на следующей схеме (рис. 12.5).

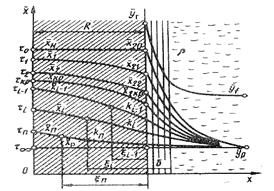
Рис.12.5. Модель массопереноса вещества в капиллярно-пористом теле

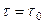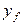В начальный момент времени концентрация распределяемого вещества постоянная во всем объеме пластины и равна . Концентрация распределяемого вещества в омывающей твердое тело фазе постоянна и равняется . При начальной концентрации вещества в твердом теле , большей равновесной концентрации, соответствующей концентрации в омывающей фазе, распределяемое вещество перемещается в омывающую фазу с поверхности раздела фаз.

При удалении свободной поверхностной влаги температура материала не меняется и равна температуре мокрого термометра, а давление паров над материалом равно давлению насыщенных паров жидкости. В этот период влага удаляется из твердого материала при постоянной скорости.

С течением времени концентрация вещества в твердом теле непрерывно снижается, принимая значения 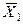, 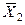. Начиная с некоторой критической концентрации 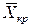, наблюдается продвижение зоны испарения в глубь тела, что приводит к уменьшению градиента потенциала переноса и к замедлению процесса.

Удаление влаги происходит не только в продвигающейся внутрь тела поверхности испарения с переменной координатой 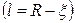, но и во всей толщине «отработанного слоя», постепенно уменьшаясь по мере приближения к поверхности тела. Это явление объясняется различными формами связи влаги с материалом.

В период уменьшения скорости общая скорость массопереноса будет определяться скоростью перемещения общего массового потока вещества от поверхности испарения к поверхности тела, т. е. скоростью массопроводности, которая определяется механизмом массопереноса.

Процесс массопроводности описывается уравнением, аналогичным закону Фика (Фурье),

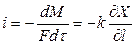, (12.30)

в котором называется коэффициентом массопроводности. Здесь Х — концентрация распределяемого вещества в твердом теле; t - температура тела.

В процессах адсорбции коэффициент массопроводности значительно зависит от степени насыщения адсорбента адсорбтивом и температуры.

В процессах экстрагирования тепловые эффекты незначительны, что позволяет рассматривать процесс массопереноса как изотермический. Это обстоятельство облегчает анализ и расчет кинетики процесса.

Наиболее сложным процессом массопереноса с твердой фазой является сушка, представляющая собой взаимосвязанный тепломассообменный процесс.

Дифференциальное уравнение массопроводности, которое выводится аналогично дифференциальному уравнению теплопроводности, имеет вид

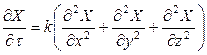. (12.31)

Условия на границе сформулируем так: к элементарной площадке на границе раздела фаз подводится из твердой фазы вещество в количестве 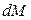, которое определяется уравнением (12.30). Это вещество отводится в омывающую фазу за cчет конвективной диффузии, т. е. 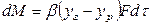. Приравнивая к этому выражению уравнение (3.1.30) и проводя преобразования, получим

/

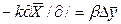Методом теории подобия получим безразмерный комплекс

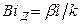, (12.32)

который называется диффузионным критерием Био.

Из уравнения массопроводности получим диффузионный критерий Фурье

Критерий Био показывает соотношение между скоростью перемещения вещества от поверхности фаз в омывающую фазу, которая характеризуется коэффициентом массоотдачи , и скоростью массопроводности.

Критерий Фурье характеризует изменение скорости массопереноса внутри твердого тела во времени.

При подобии процессов массопроводности должно соблюдаться геометрическое подобие, которое для одномерного потока выражается как 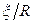, где - координата; R - определяющий размер твердого тела. Определяемой величиной является безразмерная концентрация: , где Х — концентрация в данной точке твердой фазы в момент времени .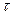

Для одномерного потока критериальное уравнение массопроводности запишется так:

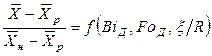. (12.34)

Аналитическое решение уравнения (12.34) имеется только для твердых тел простейшей формы: неограниченной пластины, бесконечного цилиндра и шара. Для облегчения расчетов составлены для этих тел графики, позволяющие определить по критериям 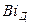и 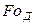безразмерные концентрации.

В зависимости от структуры капиллярно-пористого тела, режима процесса, концентрации вещества в твердой фазе стадией, определяющей скорость процесса, может быть внешний либо внутренний массоперенос либо скорость общего процесса будет определяться обеими стадиями процесса одновременно. Для характеристики влияния внутреннего и внешнего массопереноса на кинетику процесса служит значение критерия Био, которое представляет отношение внешнедиффузионного сопротивления массопереносу к внутридиффузионному.

Для описания массопередачи в системе с твердой фазой в первом приближении может быть использовано основное уравнение массопередачи (12.4).

Коэффициент массопередачи рассчитывают, например, по уравнению

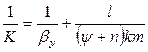, (12.35)

в котором 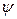- коэффициент формы, равный для пластины 1, для цилиндра 2, для шара 3; 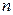- показатель степени в уравнении распределения концентраций в твердом теле.

При проведении процесса во внешнедиффузионной области, когда 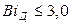, уравнение (12.35) преобразуется так:

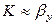. (12.36)

В этом случае скорость процесса целиком определяется внешнедиффузионными факторами.

При одновременном течении процессов тепло- и массообмена для определения коэффициентов тепломассоотдачи предложены критериальные уравнения вида

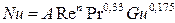, (12.37)

где: 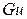- критерий Гухмана, характеризующий объемное испарение жидкости в адиабатических условиях. Значения А и 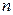зависят от гидродинамического режима в аппарате.

При 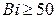лимитирующей стадией является массопроводность внутри материала и из (12.35) следует

, (12.38)

где: .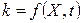

Сложность связи коэффициента массопроводности 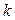с влажностью материала и температурой процесса обусловливает экспериментальное определение коэффициента массопроводности для каждого материала. Для ряда капиллярно-пористых материалов накоплено большое количество экспериментальных данных по коэффициентам массопроводности.