Обработка результатов измерений в теодолитных ходах

Результаты полевых измерений в теодолитных ходах подвергают вычислительной обработке, цель которой - получение координат вершин хода, в таком порядке. 1) Повторно выполняют все вычисления в полевых журналах. Затем на плотной бумаге с помощью транспортира и линейки составляют в произвольном масштабе схему теодолитного хода и выписывают на ней средние значения горизонтальных углов, длины сторон, углы их наклона и стрелкой показывают направление на север в начальной точке хода. 2) Дальнейшие вычисления ведут на специальном бланке «Ведомость вычисления координат вершин теодолитного хода»в последовательности:

1.Со схемы переписывают в соответствующие графы номера вершин хода (через строчку) и в те же строчки средние значения измеренных горизонтальных углов. Вычисляют горизонтальные проложения сторон, углы наклона которых больше 1° (в остальные стороны поправки за наклон не вводят, считают их равными горизонтальным проложениям) и записывают в ведомость (в строки между номерами вершин). Вычисляют их сумму – длину хода (периметр полигона), записывают ее внизу графы. В эти же строки записывают исходные дирекционные углы. В строки с номерами точек записывают координаты Х и Y исходных пунктов. 2. Вычисляют угловую невязку теодолитного хода как разность суммы измеренных углов и их теоретической суммы.

Для этого суммируют измеренные горизонтальные углы и записывают их сумму Sb_изм. внизу столбца 2, под чертой, а ниже – теоретическую сумму их, которая в замкнутом многоугольнике вычисляется по формуле:

Sb_теор. = 180°(n - 2), (6)

где n – число измеренных углов.

Для разомкнутого теодолитного хода теоретическая сумма углов вычисляется по формулам:

- для измеренных правых углов Sb_теор. = 180° n – (a_к - a_н);(9)

- для измеренных левых углов Sb_теор. = 180° n + (a_к - a_н), (10)

где , n – число измеренных углов; a_к и a_н –дирекционные углы соответственно конечной и начальной исходных сторон. Угловую невязку теодолитного хода вычисляют как разность практической (измеренной) и теоретической сумм измеренных углов

f_b = Sb_изм. - Sb_теор (7)

Сравнивают ее с допустимой, вычисляемой по формуле:

f_bдоп = ± 1’ 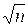. (8)

Все эти величины записывают внизу графы 2.

Если полученная невязка превышает допустимую, это означает, что имеются ошибки в вычислениях или измерениях, тогда вычисления выполняют заново и при отсутствии в них ошибок, выполняют повторно измерения.

3.Уравнивают горизонтальные углы.

Если f_b £ f_bдоп, то производится уравнивание углов, которое заключается в приведении суммы измеренных углов к теоретической их сумме путем введения поправок V_b поровну в каждый угол. Знак поправок противоположен знаку невязки. Поправки вычисляют делением невязки на число углов

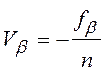. (11) Сумма поправок должна равняться невязке, взятой с противоположным знаком. Так как вычисления ведутся с округлением до 0,1¢, то не всегда невязка делится на число углов без остатка. В этом случае остаток распределяют, вводя в некоторые углы, прежде всего образованные короткими сторонами, дополнительно по 0’,1.

Например: f_b = + 2,3¢, число углов n = 5, тогда

V_b = 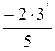= - 0,4¢ и остаток – 0,3¢.

Чтобы сумма поправок равнялась величине невязки, необходимо в три угла ввести дополнительно по – 0,1¢. Таким образом, в два угла вводят поправки по – 0,4¢ и в три по – 0,5¢, и сумма их будет равна – 2,3¢.

Если величина невязки меньше числа углов, то поправки по 0,1¢ вводят не во все углы, а в первую очередь в углы, образованные короткими сторонами, с соблюдением вышеуказанного требования равенства суммы поправок невязке, взятой с обратным знаком. Поправки записывают над измеренными углами в долях минуты со своим знаком. После этого вычисляют исправленные углы β_испр., прибавляя к измеренным углам поправки с учетом их знака

β_испр. = β_изм. + V_β.(12)

Подсчитывают сумму исправленных углов. Контролем правильности введения поправок служит равенство суммы исправленных углов их теоретической сумме, т.е. Sb_испр. = Sb_теор..

α_1-2 = α_5-1 + 180° - β₁ . (14)

Дирекционные углы записывают в строки расположенные между строками с номерами вершин теодолитного хода.

5. Вычисляют значения румбов r по формулам зависимости между ними и дирекционными углами, помня, что румб – это острый угол между стороной теодолитного хода и ближайшим к ней направлением меридиана – северным или южным, а дирекционные углы отсчитываются от северного направления оси Х.

6. Вычисление приращений координат и их уравнивание.

В соответствии с названиями румбов определяют четверть и в графы 8 и 9 записывают знаки приращений координат и вычисленные с помощью микрокалькулятора с функциями приращения координат по формулам прямой геодезической задачи:

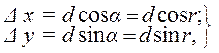(15)

Для контроля правильности измерения длин сторон в теодолитном ходе и оценки точности вычисляют невязки f_x и f_y приращений координат по координатным осям X и Y как разности между суммой вычисленных приращений и их теоретической суммой, по формулам:

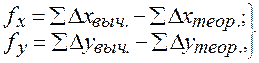(16)

Где S x_теор.= x_к – x_н ; S y_теор = y_к – y_н – разности координат конечной и начальной точек хода.

В замкнутом многоугольнике теоретическая сумма приращений координат равна нулю, поэтому невязка равна алгебраической сумме вычисленных приращений координат. Для упрощения вычислений по каждой координатной оси суммируют и записывают отдельно положительные и отрицательные суммы приращений координат, складывают их и получают невязку.

Для оценки точности измерений длин сторон в теодолитном ходе вычисляют абсолютную линейную невязку f_s хода:

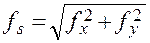, (17)

а затем относительную ошибку хода по формуле:

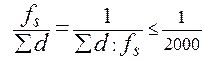. (18)

Если полученная относительная ошибка меньше допустимой 1/2000, то производят уравнивание приращений координат, а если больше, то значит имеется ошибка в вычислениях, её следует найти и устранить. Уравнивание приращений координат заключается в распределении полученных невязок в виде поправок, величины которых прямо пропорциональны длинам сторон, а знаки противоположны знакам невязок, их вычисляют по формулам:

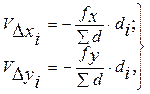(19)

где i – порядковый номер стороны теодолитного хода.

Поправки вычисляют в сантиметрах и записывают над соответствующим разрядом приращения со своим знаком

Контролем правильности вычисления поправок служит равенство их суммы невязке, взятой с обратным знаком:

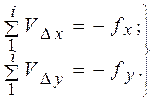(20)

Суммы поправок записывают внизу соответствующего столбца.

7.При соблюдении этого условия вычисляют исправленные приращения координат, складывая алгебраически вычисленное приращение и поправку:

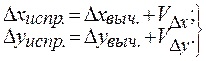(21)

Суммируют исправленные приращения координат. Контролем правильности введения поправок служит равенство суммы исправленных приращений их теоретической сумме.

8.Вычисление координат вершин теодолитного хода является заключительным действием. Их вычисляют путем последовательного алгебраического сложения координаты предыдущей точки хода с исправленным (уравненным) приращением между нею и последующей точкой по формулам:

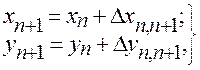(22)

где n – порядковый номер вершины хода.

Контролем правильности вычислений служит получение координат конечной точки хода. В замкнутом многоугольнике – получение координат исходной точки 1. Обработку теодолитного хода можно выполнять с использованием микроклькулятора, специальных таблиц приращении координат, либо таблиц логарифмов.