I. Исключение грубой погрешности из результатов многократных, прямых измерений.
Пусть в результате измерений получена серия значений измеряемой физической величины
А: А1; А2; А3…АN.
Для исключения грубой погрешности необходимо:
1. Провести ранжирование результатов, т.е. переписать результаты в виде возрастающей последовательности от Аmin до Аmax
2. Определить размах: R = Аmax – Аmin (8), как разность между наибольшим и наименьшим значениями этого последовательного ряда
3. Проверить результаты Аmin и Аmax на грубую погрешность, т. к. они могут резко отличаться от ожидаемых результатов по схеме:
а) рассчитать отношения:
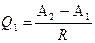 и и 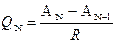
| (9) |
где (А2 – А1) - разность двух первых (соседних) результатов измерений, а (АN – АN-1) - разность двух последних результатов измерений ранжированного ряда.
б) найти 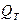 - критерий для исключения грубой погрешности из таблицы (см. стр. ) для проведенного числа опытов N и данной доверительной вероятности Р = 0,95.
- критерий для исключения грубой погрешности из таблицы (см. стр. ) для проведенного числа опытов N и данной доверительной вероятности Р = 0,95.
в) сравнить полученные отношения 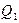 и
и 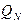 с табличным значением
с табличным значением 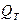 и сделать вывод о наличии грубой погрешности:
и сделать вывод о наличии грубой погрешности:
· если 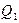 и
и 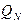
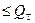 , то данная серия результатов не содержит грубую погрешность;
, то данная серия результатов не содержит грубую погрешность;
· если 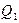 или
или 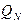 >
> 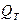 , то проверяемый результат исключается из дальнейшей обработки.
, то проверяемый результат исключается из дальнейшей обработки.
В этом случае проверяют результат А2 или АN-1 на грубую погрешность, повторяя предыдущие рассуждения.
Таблица 1
| Число наблюдений N | Доверительная вероятность Р=0,95 | ||
| QТ | t | QТ' | |
| 0,941 | 4,30 | 1,000 | |
| 0,765 | 3,18 | 0,967 | |
| 0,642 | 2,78 | 0,845 | |
| 0,560 | 2,57 | 0,736 | |
| 0,507 | 2,45 | 0,661 | |
| 0,468 | 2,37 | 0,607 | |
| 0,437 | 2,31 | 0,565 | |
| 0,412 | 2,26 | 0,531 | |
| 0,392 | 2,23 | 0,504 | |
| 0.376 | 2,20 | 0,481 |
Дата добавления: 2015-02-13; просмотров: 2658;
