Вычисление случайной погрешности

В основе определения случайной погрешности, лежат два предположения, подтверждаемые опытами:

1) при большом числе измерений случайные погрешности одинаковой величины, но разного знака встречаются одинаково часто;

2) большие погрешности встречаются реже, чем малые, то есть вероятность появления погрешности уменьшается с ростом величины погрешности.

Пусть проведено N прямых измерений физической величины A, и они не содержат грубую погрешность: A₁, A₂, A₃ … A_N.. Обозначим истинное значение данной серии измерений через A_ист, тогда абсолютная погрешность i-го измерения будем считать равной:

±DA_i=A_i-A_ист, (10)

где A_i – результат i-го измерения.

Из выражения (10) выразим абсолютные погрешности каждого из измерений

A₁, A₂, A₃ … A_N:

A₁=A_ист±DA₁

A₂=A_ист±DA₂

_{……………………}

A_N=A_ист±DA_N

Сложив почленно эти уравнения и поделив на N, получим

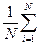A_i=A_ист± 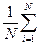DA_i (11), где

<A>= 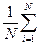A_i (12)

– среднее арифметическое значение измеренной величины.

С учётом выражения (12), наше выражение (11) примет вид:

<A>= A_ист± 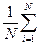DA_i (13)

Видим, что при N ® ¥ среднее значение <A> ® A_ист, так как

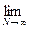
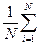DA_i ® 0.

Поэтому при многократных прямых измерениях в качестве истинного значения используют среднее арифметическое значение <A>.

Среднее арифметическое значение представляет собой то значение, относительно которого и происходит «разброс» случайных погрешностей.

В теории случайных событий (величин) характеристикой разброса случайных погрешностей является оценка среднеквадратичного отклонения результата серии измерений S, которая при ограниченном числе измерений определяется как:

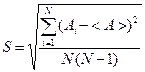(14),

где N – число измерений.

Теория вероятностей позволяет найти доверительный интервал случайной погрешности a по методу Стьюдента. Стьюдент предложил рассмотреть случайную погрешность как произведение:

a=t(p,N)*S (15),

где t(P,N) – коэффициент Стьюдента, значения которого заранее рассчитаны и приведены в таблице №1, для доверительной вероятности p=0,95.

Найти коэффициент Стьюдента можно на пересечении строки, соответствующей известному числу измерений, и столбца t(p). Если систематические и грубые погрешности устранены, то найденная величина a представляет собой случайную абсолютную погрешность a=DA и тогда результат измерения будет выглядеть так:

A=<A>±a=<A>± t(p,N)*S (16)

Это означает, что истинное значение измеряемой величины A попадает в доверительный интервал (<A>+DA ; <A>-DA) с вероятностью p=0,95, то есть 95 результатов измерений из 100 попадают в данный доверительный интервал.

Таким образом, задача нахождения случайной погрешности состоит в определении пределов вероятного изменения измеряемой величины.