ИЗМЕРЕНИЯ И ПОГРЕШНОСТИ ИЗМЕРЕНИЙ.
Существенной частью экспериментальных исследований и технологических процессов являются ИЗМЕРЕНИЯ различных физических величин. Измерения являются одним из способов познания природы, наука немыслима без измерений: «Наука начинается с тех пор, как начинают измерять...». Эти слова принадлежат основателю науки об измерениях (метрологии) в России, Д.И. Менделееву (1892 г.)
ИЗМЕРЕНИЕ- это экспериментальное сравнение данной величины с другой однородной величиной, принятой за единицу меры. Но непосредственное сравнение физической величины с ее эталоном производится редко. На практике используют различные измерительные приборы и инструменты, которые предварительно градуируются по «образцовым мерам». Разработкой системы единиц измерения физических величин, международных и государственных эталонов, качеством измерений занимаются специальные метрологические службы.
Измерения могут быть прямыми и косвенными.
При прямыхизмерениях измеряемая физическая величина непосредственно сравнивается с единицей измерения с помощью приборов и устройств, проградуированных в соответствующих единицах. К прямым измерениям относятся, например, измерение линейных размеров с помощью линейки, штангенциркуля, или измерения при помощи электроизмерительных приборов, например, измерение силы тока амперметром, напряжения - вольтметром, сопротивления - омметром и т. д.
При косвенных измерениях измеряется не сама величина, другие величины, функционально связанные с измеряемой величиной. Сама же искомая величина рассчитывается с помощью этой функциональной зависимости. К косвенным измерениям относится, например, измерение объема тела по его размерам, скорости через путь и время и т. д.
Суть измерений заключается в получении количественной информации о качественном свойстве измеряемого объекта опытным путем с помощью специальных технических средств. А само значение физической величины называется результатом измерения.
Общее уравнение измерений имеет вид:
| А = n [A] | (1) |
где А - измеряемая физическая величина,
[A] - единица измерения физической величины,
n - числовое значение физической величины.
Любое измерение не дает абсолютно точного значения измеряемой величины, как и не существует абсолютно точных способов измерений, абсолютно точных приборов, так как всегда имеются причины, в той или иной степени искажающие результат.
Абсолютно точное значение измеряемой величины называют ИСТИННЫМ значением, которое самым идеальным образом отображает как в количественном, так и в качественном отношениях соответствующее свойство объекта. То есть в результате измерения мы никогда не сможем определить истинное значение величин, а получаем лишь приближенное значение, отличающиеся от истинного. И чем меньше отличие результата измерений от истинного значения, тем выше точность измерения. Точность измерения - это степень приближения результата измерения к его истинному значению. А само отличие, т. е. отклонение результата измерения от истинного значения, называют ошибками или погрешностями измерения.
Если измеряемая физическая величина А имеет истинное значение Аист, а результат измерения А, то абсолютная погрешность будет равна:
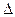 А = |А - А = |А - 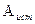 | |
| (2) |
Очевидно, что абсолютная погрешность измеряется тех же единицах измерения, что и сама физическая величина, т.е. абсолютная погрешность измерения является величиной, обладающей размерностью.
Для сравнения точности измерений с самой измеренной физической величиной вводят понятие относительной погрешности, которая равна отношению абсолютной погрешности к истинному значению физической величины:
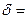 = = 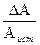
| (3) |
Обычно относительную погрешность выражают в процентах:
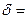 = = 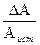 ×100% ×100%
| (4) |
Т. к. истинное значение измеряемой величины остаётся нам неизвестным, то абсолютная погрешность 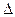 А (см. Формулу (2)) является приближенной оценкой. Можно утверждать, что истинная абсолютная погрешность меньше
А (см. Формулу (2)) является приближенной оценкой. Можно утверждать, что истинная абсолютная погрешность меньше 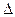 А или больше
А или больше 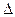 А. Следовательно, мы можем только указать с некоторой вероятностью Р < 1, что истинное значение измеряемой физической величины находится внутри некоторого интервала, величину которого графически можно изобразить следующим образом:
А. Следовательно, мы можем только указать с некоторой вероятностью Р < 1, что истинное значение измеряемой физической величины находится внутри некоторого интервала, величину которого графически можно изобразить следующим образом:
А - 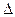 А < А < 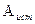 < А + < А + 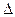 А А
| (5) |
Указанный интервал (5) называется доверительным интервалом, а вероятность Р - доверительной вероятностью. Доверительная вероятность приблизительно равна доле измерений, результаты которых попадают в этот интервал, т. е. отличаются от истинного значения на величину не большую чем 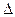 А.
А.
Дата добавления: 2015-02-13; просмотров: 1346;
