Абсолютная и относительная погрешности

С приближенными числами нам приходится иметь дело при вычислениях значений каких-либо функций, либо при измерениях и обработке физических величин, получаемых в результате экспериментов. В том и другом случае нужно уметь правильно записывать значения приближенных чисел и их погрешность.

Приближенным числом а называется число, которое незначительно отличается от точного числа А и заменяет последнее в вычислениях [6]. Если известно, что а < А, то а называется приближенным значением числа А по недостатку; если а > А, – то по избытку. Если а есть приближенное значение числа А, то пишут а ≈ А.

Под ошибкой или погрешностью А приближенного числа а обычно понимается разность между соответствующим точным числом А и данным приближенным, т.е.

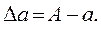
Чтобы получить точное число А, нужно к приближенному значению числа прибавить его ошибку 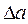, т.е.

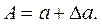
Во многих случаях знак ошибки неизвестен. Тогда целесообразно пользоваться абсолютной погрешностью приближенного числа

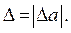
Из приведенной записи следует, что абсолютной погрешностью 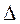приближенного числа а называется модуль разности между соответствующими точным числом А и его приближенным значением а, т.е.

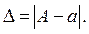(1.1)

Точное число А чаще всего бывает неизвестно, поэтому найти ошибку или абсолютную погрешность не представляется возможным. В этом случае полезно вместо неизвестной теоретической погрешности 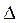ввести ее оценку сверху, так называемую предельную абсолютную погрешность.

Под предельной абсолютной погрешностью приближенного числа а понимается всякое число 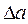, не меньшее абсолютной погрешности этого числа, т.е.

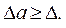
Если в последней записи вместо 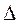использовать формулу (1,1), то можно записать

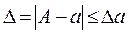(1.2)

Отсюда следует, что точное число А заключено в границах

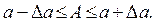Следовательно, разность 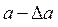есть приближение числа А по недостатку, а 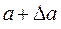– приближение числа А по избытку. В этом случае для краткости пользуются записью

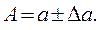
Ясно, что предельная абсолютная погрешность определяется неоднозначно: если некоторое число есть предельная абсолютная погрешность, то любое большее, чем 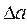положительное число, тоже есть предельная абсолютная погрешность. На практике стараются выбирать возможно меньшее и простое по записи число 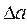,удовлетворяющее неравенству (1.2).

Например, если в результате измерения получили длину отрезка l = 210 см ± 0,5 см., то здесь предельная абсолютная погрешность 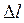= 0,5 см, а точная величина l отрезка заключена в границах 209,5см≤l≤210,5см.

Абсолютная погрешность недостаточна для характеристики точности измерения или вычисления. Так, например, если при измерении длин двух стержней получены результаты l₁ = 95,6см ± 0,1см и l₂ =8,3 ± 0,1 см, то, несмотря на совпадение предельных абсолютных погрешностей, точность первого измерения выше, чем второго. Отсюда видно, что для точности измерений важнее не абсолютная, а относительная погрешность, которая зависит от значений измеряемых величин.

Относительной погрешностью δ приближенного числа а называется отношение абсолютной погрешности 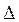этого числа к модулю соответствующего точного числа А, т.е.

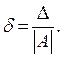
Аналогично предельной абсолютной погрешности используют также определение и для предельной относительной погрешности. Предельной относительной погрешностью 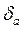данного приближенного числа а называется всякое число, не меньшее относительной погрешности этого числа

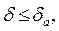
т.е. 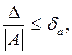откуда следует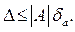

Таким образом, за предельную абсолютную погрешность числа а можно принять

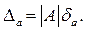(1.3)

Так как на практике А≈а,то вместо формулы (1.3) часто пользуются формулой

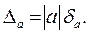
1.2 Десятичная запись приближенных чисел

Всякое положительное десятичное число а может быть представлено в виде конечной или бесконечной дроби

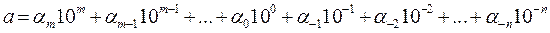(1.4)

где 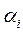– десятичные цифры числа а ( 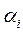= 0,1,2,...,9), причем старшая цифра 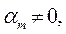а m – число разрядов в записи целой части числа а, а n – число разрядов в записи дробной части числа а. Например:

5214,73... = 5 · 10³ + 2 · 10² + 1 · 10¹ + 4 · 10⁰ +7 · 10^-1 + 3 · 10^-2... (1.5)

Каждая цифра 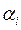, стоящая на определенном месте в числе а, написанном в виде (1.4), имеет свой вес. Так, цифра, стоящая на первом месте (т.е. 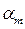), весит 10^m, на втором – 10^m-1 и т.д.

На практике мы обычно не пользуемся записью в форме (1.4), а используем сокращенную запись чисел в виде последовательности коэффициентов 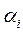при соответствующих степенях 10. Так, например, в записи (1.5) мы пользуемся левой от знака равенства формой, а не правой, представляющей разложение этого числа по степеням 10.

На практике преимущественно приходится иметь дело с приближенными числами в виде конечных десятичных дробей. Для корректного сравнения различных вычислительных и экспериментальных результатов вводят понятие значащей цифры в записи результата. Все сохраняемые десятичные значения 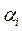(i = m, m-1,…, m-n+1), отличные от нуля, и нуль, если он стоит между значащими цифрами или является представителем сохраненного десятичного разряда в конце числа называются значащими цифрами приближенного числа а. При этом нули, связанные с множителем 10ⁿ к значащим не относятся.

При позиционном обозначении числа а в десятичной системе счисления иногда приходится вводить лишние нули в начале или в конце числа. Например,

а = 7·10^-3 + 0·10^-4 + 1·10^-5 + 0·10^-6 = 0,007010

или

b = 2·10⁹ + 0·10⁸ + 0·10⁷ + 3·10⁶ + 0·10⁵ = 2003000000.

Такие нули (в приведенных примерах они подчеркнуты) не считаются значащими цифрами.

Значащей цифрой приближенного числа называется всякая цифра в его десятичном изображении, отличная от нуля, а также и нуль, если он содержится между значащими цифрами или является представителем сохраненного десятичного разряда. Все остальные нули, входящие в состав приближенного числа и служащие лишь для обозначения его десятичных разрядов, не причисляются к значащим числам.

Например, в числе 0,002080 первые три нуля не являются значащими цифрами, так как они служат только для установления десятичных разрядов других цифр. Остальные два нуля являются значащими цифрами, так как первый из них находиться между значащими цифрами 2 и 8, а второй указывает на то, что в приближенном числе сохранен десятичный разряд 10^-6. В случае, если в данном числе 0,002080 последняя цифра не является значащей, то это число должно быть записано в виде 0,00208. С этой точки зрения числа 0,002080 и 0,00208 не равноценны, так как первое из них содержит четыре значащих цифры, а второе лишь три.

Кроме понятия значащей цифры важным является понятие верной цифры. Следует отметить, что это понятие существует в двух определениях – в узком и широком смыслах.

Определение(в широком смысле).Говорят, что n первых значащих цифр числа (считая слева направо) являются верными в широком смысле, если абсолютная погрешность этого числа не превосходит единицы (веса) n-горазряда. (Пояснение: 1 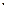10¹ – здесь вес 1 равен 10; 1 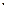10⁰ – здесь вес 1 равен 1; 1 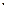10^-1 – здесь вес 1 равен 0,1; 1 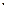10^-2 – здесь вес 1 равен 0,01 и т.д.).

Определение(в узком смысле). Говорят, что n первых значащих цифр приближенного числа являются верными, если абсолютная погрешность этого числа не превосходит половины единицы (веса) n-горазряда. (Пояснение: 1 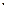10¹ – здесь вес половины 1 равен 5; 1 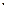10⁰ – здесь вес половины 1 равен 0,5; 1 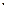10^-1 – равен 0,05 и т.д.).

Например, в приближенном числе 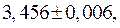исходя из первого определения, значащие цифры 3,4 и 5 верные в широком смысле, а цифра 6 – сомнительна. Исходя из второго определения, значащие цифры 3 и 4 являются верными в узком смысле, а цифры 5 и 6 – сомнительные. Важно подчеркнуть, что точность приближенного числа зависит не от количества значащих цифр, а от количества верных значащих цифр.

Как в теоретических рассуждениях, так и в практических применениях большее применение находит определение верной цифры в узком смысле.

Таким образом, если для приближенного числа а, заменяющего число А, известно, что

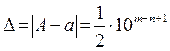(1.6)

то, по определению, первые n цифр 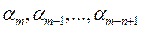этого числа являются верными.

Например, для точного числа А = 35,97 число а = 36,00 является приближенным с тремя верными знаками. К этому результату приводят следующие рассуждения. Так как абсолютная погрешность нашего приближенного числа составляет величину 0,03, то по определению она должна удовлетворять условию

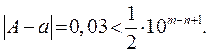(1.7)

В нашем приближенном числе 36,00 цифра 3 является первой значащей цифрой (т.е. 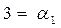), поэтому m = 1. Отсюда очевидно, что условие (1.7) будет выполняться при n = 3.

Обычно принято при десятичной записи приближенного числа писать только верные цифры. Если известно, что данное приближенное число записано правильно, то по записи можно определить предельную абсолютную погрешность. Именно при правильной записи абсолютная погрешность не превышает половины младшего разряда, который следует за последним верным разрядом (или половины единицы последнего верного разряда, что одно и то же)

Например, даны приближенные числа, записанные правильно: а = 3,8; b = 0,0283; с = 4260. Согласно определению, предельные абсолютные погрешности этих чисел будут: 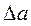= 0,05; 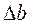= 0,00005; 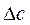= 0,5.