Связь относительной погрешности приближенного числа с количеством верных знаков

Теорема (без доказательства). Если положительное приближенное число а имеет п верных десятичных знаков, то относительная погрешность 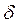этого числа не превосходит величину 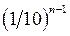, деленную на первую значащую цифру данного числа, т.е.

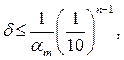
где 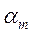– первая значащая цифра числа а.

За предельную относительную погрешность числа a можно принять

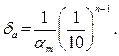
Если число а имеет больше двух верных знаков, т.е. п ≥ 2, то практически справедлива формула

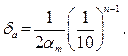(1.8)

Пример. Какова будет предельная относительная погрешность, если вместо числа π использовать а = 3,14?

Решение. В нашем случае 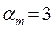и п = 3, поэтому

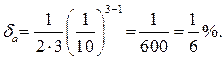
Для решения обратной задачи определения количества верных знаков числа а, если известна его относительная погрешность, обычно пользуются приближенной формулой

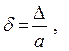
где 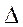– абсолютная погрешность числа а (а > 0). Отсюда

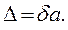(1.9)

Если

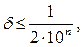
то число а имеет п верных знаков, что следует из формулы (1.6)

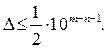
Пример. Приближенное число а = 24253 имеет относительную точность 1%. Сколько в нем верных знаков?

Решение. Исходя из абсолютной погрешности, определяемой формулой (1.9), запишем

Δ = 24253 ∙ 0,01 ≈ 243 = 2,43 ∙ 10².

В заданном числе а = 24253 первой значащей цифре 2 соответствует m = 4. Поэтому можем записать

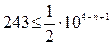или .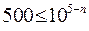

Из последнего неравенства следует, что оно может выполняться лишь при n = 2. Следовательно, в числе а будут верными лишь первые две цифры.

1.5. Погрешность суммы и разности приближенных чисел

Предельная абсолютная погрешность алгебраической суммы нескольких приближенных чисел равна сумме предельных абсолютных погрешностей этих чисел.

Пример 1. a₁= 25,74 ± 0,02; a₂ = 96,42 ± 0,03; a₁ + a₂ = 122,16 ± 0,05,т.е. | Δ_Σ | = | Δа₁|+| Δа₂| = 0,02 + 0,03 = 0,05.

Пример 2. и = 2,72 + 3,00 + 2,11 = 7,83;Δи=0,005+0,005+0,005=0,015.

Округляя до одного знака после запятой и учитывая погрешность округления, получим и = 7,8±0,015, т.е. в записи и = 7,8 все цифры верны.

Пример 3. Необходимо сложить два приближенных числа 265 и 32. Пусть предельная погрешность первого числа равна 5, а второго – 1. Тогда предельная погрешность суммы равна 6. Так, если истинное значение первого числа есть 270, а второго 33, то приближенная сумма будет 265 + 32 + 297, т.е. она на 6 единиц меньше истинной 270 + 33 = 303.

Пример 4.Найти сумму приближенных чисел

0,0909 + 0,0833 + 0,0769 + 0,0714 + 0,0667 + 0,0625 + 0,0588 +0,0556 + 0,0526.

Результатом сложения является число 0,6187. Поскольку предельная погрешность каждого слагаемого есть 0,00005, то предельная погрешность суммы будет 0,00005 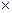9 = 0,00045. Значит, в последнем (четвертом) знаке суммы возможна ошибка до 5 единиц. Поэтому округляем сумму до третьего знака, т.е. до тысячных. В результате получаем число 0,619, в котором все три цифры являются верными.

При значительном числе слагаемых обычно происходит взаимная компенсация погрешностей. Поэтому истинная погрешность суммы лишь в исключительных случаях совпадает с предельной погрешностью или близка к ней. Иначе говоря, при значительном числе суммирования приближенных чисел их сумма, как правило, гораздо точнее слагаемых. Это происходит благодаря взаимной компенсации погрешностей суммируемых чисел.

Теперь рассмотрим погрешность разности двух приближенных чисел.

Исходя из понятия абсолютной величины любого числа, нетрудно заключить, что предельная абсолютная погрешность разности приближенных чисел также как и для суммы двух приближенных чисел, равна сумме предельных абсолютных погрешностей уменьшаемого и вычитаемого.

Пример 5. Пусть предельная погрешность приближенного уменьшаемого 85 равна 2, а предельная погрешность вычитаемого 32 равна 3. Предельная погрешность разности 85 – 32 = 53 есть 2 + 3 = 5. Действительно, истинные значения уменьшаемого и вычитаемого могут равняться 85 + 2 = 87 и 32 – 3 = 29. Тогда истинная разность будет 87 – 29 = 58. Она на 5 единиц отличается от приближенной разности, равной 53.

Однако надо иметь ввиду, что в противоположность сумме разность приближенных чисел может быть менее точной, чем уменьшаемое и вычитаемое отдельно взятые. Эффект «потери точности» особенно велик в том случае, когда уменьшаемое и вычитаемое мало отличаются друг от друга.

Пример 6.Измерение внешнего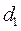и внутреннего 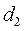диаметров тонкостенной трубки дало результаты 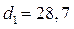мм, 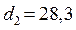мм. Вычислим по этим данным толщину стенки трубки. Предельная абсолютная погрешность уменьшаемого и вычитаемого одна и та же: 0,05. Относительная погрешность уменьшаемого 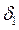и вычитаемого 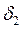тоже примерно одинакова, а именно:

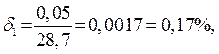
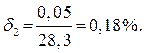
Толщина стенки трубки 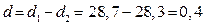мм. Предельная абсолютная погрешность числа 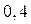тоже будет 0,05, а относительная погрешность уже составит величину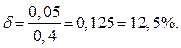

<1 2 345 6 7 >

Дата добавления: 2015-02-03; просмотров: 6490;