Метод ветвей и границ с использованием
Таблицы покрытий
Рассмотрим применение этого метода на том же примере, для чего воспроизведём таблицу покрытий для диагностики однократных неисправностей (см.табл. 3.13 ).
Таблица 3.14
Таблица покрытий для диагностики однократных неисправностей
| {p} | S1S2 | S1S3 | S1S4 | S1S5 | S2S3 | S2S4 | S2S5 | S3S4 | S3S5 | nj |
| U1 | U2 | U3 | U4 | U5 | U6 | U7 | U8 | U9 | ||
| p1 p3 p4 p5 p7 | ||||||||||
| p8 p9 p10 p11 p12 | ||||||||||
| Pui | 0,0661 | 0,0447 | 0,0313 | 0,0183 | 0,00497 | 0,00348 | 0,00204 | 0,00235 | 0,00138 |
На первом шаге построения усечённого дерева решений мы должны выбрать первую элементарную проверку, с которой начнётся построение дерева решений. Для выбора первой проверки имеются следующие рекомендации:
- если имеется ядро теста (признаком чего является наличие только одной единицы хотя бы в одном столбце), то первой должна выбираться элементарная проверка, входящая в ядро теста, причём, если ядро состоит из нескольких элементарных проверок, то должна выбираться либо та, которая содержит максимальное число единиц, либо имеющая минимальную стоимость ;
- если ядра теста не существует, то первой должна выбираться проверка, имеющая максимальное число единиц, а если таковых несколько, то из них выбирается проверка, характеризуемая минимальной стоимостью.
В нашем случае ядра теста не существует и имеется 6 элементарных проверок с максимальным числом единиц (6). Из них минимальной стоимостью характеризуется элементарная проверка p3 (они расположены и пронумерованы в нашей таблице в порядке возрастания их стоимости).
Следовательно на первом шаге выбираем проверку p3. Теперь вычеркнем из таблицы покрытий все столбцы, покрываемые строкой p3 и саму эту строку. В результате получаем табл. 3.15.
Таблица 3.15.
Таблица покрытий после первого шага
| pj | U2 | U3 | U7 | U8 | Nj |
| p1 p4 p5 p7 p8 p9 p10 p11 p12 |
В ней оказались одинаковые строки : p5 и p11; p8 и p9. Из них оставим строки с меньшей стоимостью (т.е. вычеркнем строки p11 и p9). В итоге в таблице остаётся 4 столбца и 7 строк.
Теперь приступим к вычислению нижней границы непостроенной части теста. Для этого необходимо расположить все строки в порядке убывания в них числа единиц Ù p5,p7,p8,p1,p4,p10,p12.
Нижняя граница (т.е. длина) непостроенной части теста определяется из соотношений :
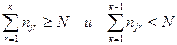 (3.6)
(3.6)
где: N – число столбцов в усечённой таблице покрытий ( в нашем примере N=4) ;
njr – число единиц в строках, расположенных в порядке убывания в них числа единиц (причём индекс r означает новую нумерацию строк, расположенных в указанном порядке). Подставляя значения к от единицы и выше определяем такое значение к, при котором неравенства (3.6) выполняются. В нашем примере к=2, т.к.
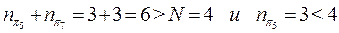
При любых других к неравенства не выполняются.
Полученное значение к и представляет собой нижнюю границу непостроенной части теста. Т.е. для построения минимального теста необходимы ещё две элементарные проверки (кроме уже выбранной).
Метод ветвей и границ позволяет определить нижнюю границу теста и для альтернативного случая, когда в качестве первой выбирается любая из оставшихся элементарных проверок, т.е. не проверка p3, а какая-то другая. Причём не конкретизируется какая именно из них будет выбрана. Для этого удалим строку p3 из исходной таблицы покрытий (не удаляя покрываемых ей столбцов). Поскольку все столбцы остались, то и одинаковых строк не будет, а значит нумерация строк в порядке убывания числа единиц будет:
| pj | p5 | p7 | p8 | p9 | p11 | p1 | p4 | p10 | p12 |
| nj | |||||||||
| r |
а N=10.
В соответствии с неравенствами (3.6) определяем к=2 : 6+6=12>10 , 6<10.
Это говорит о том, что среди оставшихся элементарных проверок могут быть такие две, которые совместно покрывают все столбцы. И действительно, неравенства (3.6) указывают лишь на то, что сумма единиц в отобранных проверках должна быть не меньше числа столбцов. Но это вовсе не значит, что такая пара действительно существует в данной таблице покрытий. И действительно, в нашей таблице покрытий (даже с учётом проверки p3) нет такой пары проверок, которая бы покрывала все столбцы. Кроме того, число проверок в тесте должно быть достаточно для однозначной идентификации всех диагностируемых состояний. В нашем случае объект имеет 5 диагностируемых состояний, для идентификации которых необходимо как минимум иметь 3 двоичных разряда (каждая элементарная проверка даёт значение одного двоичного разряда). Поэтому двух проверок в любом случае недостаточно.
Теперь продолжим построение теста. На втором шаге необходимо из усечённой на первом шаге таблицы покрытий выбрать очередную проверку. Выбор следует производить из проверок, имеющих максимальное число единиц. Это проверки p5,p7 и p8, имеющие по 3 единицы. Выбираем из них p5, как обладающую наименьшей стоимостью. В таблице 3.15 вычёркиваем строку, соответствующую p5, и покрываемые ею столбцы. В результате в таблице остаётся лишь один столбец u3 который покрывает проверки p1,p4,p7 и p8. Поэтому на третьем шаге мы можем выбрать любую из этих проверок. Выбираем самую дешёвую p1, чем и завершаем построение оптимального (или близкого к оптимальному) теста, который будет состоять из проверок p3p5p1. Причём в безусловных тестах их порядок не имеет значения. В условных тестах наивыгоднейшим является порядок : p5,p3p1. Но в этом случае нельзя утверждать, что это будет оптимальный тест.
Идентификаторами состояния объекта будут являться двоичные слова, получаемые в результате проведения элементарных проверок, вошедших в тест, которые можно определить из таблицы состояний (табл. 3.12). для теста p1p3p5 мы получаем
S1 – 111
S2 – 100
S3 – 110
S4 – 011
S5 – 101
Теперь сравним полученный тест с теми, которые мы получили с помощью инженерно-логических методов. Для безусловных тестов полученные тесты полностью совпали. Но оптимальный условный тест вместо проверки p1 должен включать проверку p4, причём порядок следования проверок задаётся жёстко : p4p3p5.
Дата добавления: 2017-03-29; просмотров: 660;
