В этой таблице две пары проверок (p1 и p2) и (p3 и p4) получились одинаковыми. Поэтому проверки p2 и p6 удалим, сохранив нумерацию остальных проверок.

Теперь образуем все пары состояний объекта (Si,Sk) и рассчитаем их вероятности: .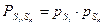

При построении таблицы покрытий элементарные проверки будем располагать в виде строк, а пары состояний – в виде столбцов. В клетках таблицы будем записывать нуль, если данная проверка не различает данную пару состояний (т.е. даёт одинаковые результаты – или нули, или единицы) и будем записывать единицу, если проверка различает данную пару состояний (для одного из состояний проверка даёт 0, для другого – 1, или наоборот). В итоге получаем табл.3.13.

Таблица 3.13

Таблица покрытий

{p}	S1 S2	S1S3	S1S4	S1S5	S2S3	S2S4	S2S5	S3S4	S3S5	S4S5
U1	U2	U3	U4	U5	U6	U7	U8	U9	U10
p1 p3 p4 p5 p7
p8 p9 p10 p11 p12
Pu	0,0661	0,0447	0,0313	0,0183	0,00497	0,00348	0,00204	0,00235	0,00138	0,00097

В ней уже нет одинаковых строк и дальнейшее упрощение таблицы покрытий может производиться за счёт поглощения одной из строк другой. Это возможно в том случае, если поглощающая строка содержит единицы во всех тех столбцах, где есть единицы в поглощаемой строке и, кроме того, имеет хотя бы одну дополнительную единицу. Но в данном случае таких упрощений провести нельзя, т.к. отсутствуют поглощаемые строки.

Поскольку в этой таблице нет нулевых столбцов, то это означает, что совокупность данных элементарных проверок позволяет различить все пары состояний, т.е. обеспечивает необходимую глубину диагностики. Однако насколько данный тест, состоящий из 10 элементарных проверок будет избыточен сказать пока нельзя. Для этого мы должны на основе данной таблицы покрытий построить оптимальный тест. Воспользуемся для этого теми же методами, которые ранее использовались для построения оптимального теста на основе таблицы состояний.

3.4.2. Построение оптимального теста с использованиемфункций предпочтения ( инжененерно-логический метод )

Поскольку в данном случае рассчитаны вероятности всех пар состояний и заданы стоимости всех элементарных проверок, то функции предпочтения будут состоять в следующем (для безусловных тестов с безусловной остановкой ):

1) для получения минимального (наиболее короткого) теста необходимо отбирать элементарные проверки с максимальным числом единиц, причём при выборе последующих проверок единицы должны быть в тех столбцах, в которых содержались нули в уже отобранных проверках;

2) если в соответствии с п.1 конкурируют несколько элементарных проверок, то следует отдавать предпочтение проверке с минимальной стоимостью.

Для условных тестов и безусловных тестов с условной остановкой в дополнение к уже перечисленным функциям предпочтения необходимо учитывать ещё одну :

3) в первую очередь следует отбирать проверки, различающие пары состояний, характеризуемые максимальной вероятностью ;

Построим сначала безусловный тест с безусловной остановкой.

Для выбора первой элементарной проверки подсчитаем число единиц в каждой строке таблицы покрытий и выделим те, которые содержат максимальное число единиц. Таких проверок у нас 6: p3,p5,p7,p8,p9,p11. Все они содержат по 6 единиц. Выбираем в качестве первой проверку p3, как обладающую минимальной стоимостью из перечисленных. Она покрывает столбцы u1,u4,u5,u6,u9 и u10.

В качестве следующей должна быть выбрана проверка, покрывающая максимальное число ещё некоторых столбцов (u2,u3,u7,u8). Из таблицы видно, что есть проверки, покрывающие три из четырёх пустых столбцов. Это проверки :p₅(u₂,u₇,u₈),p₇(u₂,u₃,u₇),p₈(u₃,u₇,u₈),p₉(u₃,u₇,u₈),p₁₁(u₂,u₇,u₈). Из них выбираем проверку с минимальной стоимостью p₅, покрывающую столбцы (u₂,u₇,u₈). После этих двух проверок непокрытым оказывается лишь один столбец u₃. Поэтому третьей может быть взята любая проверка, имеющая единицу в данном столбце. Выбираем из них самую дешёвую проверку p₁.

Итак, оптимальный безусловный тест должен содержать три проверки p₁,p₃ и p₅ (в безусловных тестах очередность отобранных проверок не играет роли).

Теперь построим безусловный тест с условной остановкой. Теперь при выборе каждой элементарной проверки необходимо учитывать ещё и вероятности распознаваемых ей состояний. Поэтому в качестве первой следует выбрать проверку p₄, которая содержит единицу в первых четырёх столбцах или проверку p_7, которая содержит единицы в столбцах со 2-го по 7-й. В первом случае суммарная вероятность распознаваемых состояний равна 0,16, а во втором – 0,105.

Таким образом, предпочтительней проверка p₄, хотя она и содержит на две единицы меньше. К тому же она и дешевле, чем p₇.

Далее следует выбирать проверку, покрывающую максимальное число столбцов, начиная с пятого (причём желательно подряд). Здесь следует рассмотреть проверки p₃,p₅,p₈,p₁₁, перекрывающих по 4 из 6 пустых столбцов (но не подряд) и проверки p₇ и p_12, перекрывающих подряд 3 столбца, начиная с с 5-го. Подсчитаем суммарные вероятности тех пар состояний, которые они различают: p₃®Sр=0,0108, p₅®Sр=0,00925,p₈®Sр=0,0103,p₉®Sр=0,00925,p₁₁®Sр=0,0103, p₇®Sр=0,0105. Как видим, с этих позиций наилучшей является проверка p₃. К тому же она и минимальна по стоимости. Поэтому следует выбрать её.

После этих двух проверок пустыми остаются лишь два столбца u₇ и u₈. Поэтому выбираем самую дешёвую проверку, покрывающую эти столбцы. Это проверка p₅.

Итак, условный тест будет: p₃p₄p₅, причём здесь их уже нельзя менять местами.

Опознавателями отдельных состояний при выполнении тестирования будут являться результатом данных проверок по таблице состояний:

для теста p₁p₃p₅: для теста p₄p₃p₅:

S₁ (1111) – 111 S₁ – 111

S₂ (1110) – 100 S₂ – 000

S₃ (1011) – 110 S₃ – 010

S₄ (0111) – 011 S₄ – 011

S₅ (1101) – 101 S₅ – 001

Из анализа опознавателей для безусловного теста с условной остановкой следует, что уже по результатам первой проверки p₄, мы можем опознавать первое (исправное) состояние объекта. Для распознавания же всех начальных состояний необходимо выполнить остальные две проверки.

Очевидно, что и условный тест в данном случае будет состоять из тех же проверок и характеризоваться следующим деревом решений:

Рис. 3.5.Дерево решений условного теста

В данном дереве решений по сравнению с предыдущим тестом на третьем шаге в левой ветви дерева проверка p₅ заменена на более дешёвую p₁.

Теперь рассчитаем показатели эффективности данных тестов.

Стоимость тестирования с помощью безусловного теста с безусловной остановкой будет постоянна (независимо от действительного состояния объекта) и складываться из стоимости входящих в него проверок:

С_бб=С₁+С₃+С₅=22+27+35=84

Стоимость тестирования безусловным тестом с условной остановкой будет зависеть от действительного состояния объекта, а потому должна характеризоваться средней стоимостью:

С_бу=С4Ps₁+(C₄+C₃+C₅)(Ps₂+Ps₃+Ps₄+Ps₅)=31*0,7713+(31+27+35)* *(0,0857+0,0580+0,0406+0,0238)=23,91+94*0,208=43,47.

Средняя стоимость тестирования условным тестом будет:

Су=С4Ps₁+(C₄+C₃+C₁)(Ps₃+Ps₄)+(C₄+C₃+C₅)(Ps₂+Ps₅)=31*0,7713+(31+27+22)(0,058+0,0406)+(31+27+35)(0,0857+0,0238)=

=23,91+80*0,0986+ +94*0,1095=23,91+7,89+10,29=42,09

Как видим, выигрыш в стоимости условным тестом (или безусловным тестом с условной остановкой) получается существенным – в два раза. При этом разница в средней стоимости тестирования условным тестом и безусловным тестом с условной остановкой несущественна.